

3 - THE TRIPLE MARKER
Abstract: It transpires that an eye-catching event, set in the infinite series of triangular numbers, turns out to be the confluence of many more singular features of interest. Significant items of biblical data are found to map precisely onto these. Clearly, the implications of a coincidence of this magnitude are enormous, and far-reaching.
[Note: a number of links to supportive material are offered in this account; since many were written as appendices to other pages their identifying numbers are not relevant to the present context, and should be ignored.]
1. Introduction
Those in search of absolute truth in this world need look no further than the Book of Number where subsets of the natural (or, counting) numbers provide relationships that none can gainsay. The figurate numbers associate familiar regular 2-D and 3-D shapes with specific sequences that are limitless in extent, and these provide a dependable framework within which many other universal and eternal verities may be deduced. Operating together with these numerical fundamentals are the patterns of digits which arise from their symbolic representation - particularly as denary (or base 10) objects. Our purpose here is to demonstrate that significant items of biblical data map precisely onto certain rare features of the triangular series and its derivatives - the suggestion being that these 'coincidences' have been purposely engineered to convince all thinking people of the reality of our Creator's Being and Sovereignty, and of the integrity of His revelation to man - the Judeo-Christian Scriptures.
[Note: In this presentation, the tables of numerical data derive from a series of Visual Basic investigations involving 'long' integers over the range 1 - 2,147,483,647 ( = 2^31 - 1). Included within this range are 65535 triangles - representing a mere 0.003% of the total.]
2. Triangular numbers: a quick recap
It is appropriate that we first prepare the ground so that the facts which follow may be properly understood. Triangular numbers are simple derivatives of the natural, or counting numbers. Here, in Figure 1 are the opening terms of the general triangle series (T), and of an important subset of the same - the generator triangles (G).
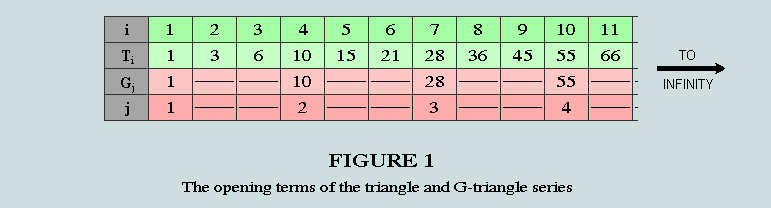
Observe that T(i) is the cumulative total of the triangle order numbers from 1 to i, inclusive. Or, putting it another way, the ith triangle is the sum of the numbers named when counting to i.
G-triangles will already be familiar to readers of these pages; they form a substantial subset of the triangular numbers: beginning with 1 - the degenerate first term of the series - they subsequently occupy every 3rd position, ad infinitum.
[Note: the position of the jth G-triangle in the general series is given by i = 3j - 2; conversely, provided the ith of the general series is a G, then ,j = (i + 2) / 3]
Other features of G-triangles include:
all are built around a single centroid counter (rendered white in the following figures), and each is capable of generating a symmetrical hexagon/hexagram pair - designated X/Y - by self-intersection/-union, in the manner depicted in the following example:
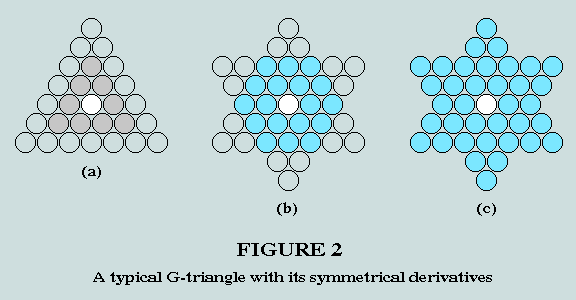
Here, at (a), we have a representation of the 3rd G-triangle(which corresponds with the7th of the general series); (b) depicts the hexagon formed by the intersection of this triangle with an inverted copy of itself; and (c), the hexagram represented by the union of these triangles.
[Observe that the order of a G-triangle = the number of triangular 'rings' surrounding the centroid counter, plus 1.]
Each G-triangle is essentially a composite of 9 smaller congruent elemental triangles (drawn from the general series) disposed symmetrically about the centroid counter - in the manner depicted here:
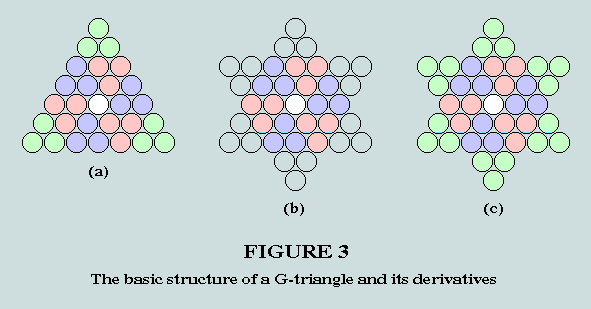
This multicoloured presentation enables us to clearly identify the elementals within each structure represented. Observe that hexagon (b) and hexagram (c) comprise 6 and 12 of these, respectively.
[Note: The relationships between parent G-triangle and elemental are straightforward: subtracting 1 from the order of a G-triangle yields the order of the elemental; subtracting 1 from the value of the parent, and dividing the result by 9, yields the value of the elemental.]
Expressed symbolically in the usual way (i.e. in denary notation) the ultimate sum of the digits of a G-triangular number is 1. As an example, consider the number 991081981 (which occupies position 44521 in the general triangle series, and position 14841 in the G-triangle series). The sum of its digits is 46; the sum of the digits of 46 is 10; the sum of the digits of 10 is 1. This feature enables us to quickly determine whether or not a given triangle is G.
[Note: further information on basics of numerical geometry may be found here.]
3. Five sparse subsets of the general triangle series
Attention is drawn to the following:
Those triangles which, as denary objects, exhibit reversibility - remaining triangular when the order of their digits is reversed. Such numbers are typically palindromic (in which case, it is the same triangle that results from the digit reversal), but others provide a different triangular outcome. These are here collectively termed R-triangles.
Those triangles which, when doubled, produce a triangular result. These are here referred to as X2-triangles (i.e. 'times 2'-triangles).
Those triangles which, when tripled, produce a triangular result. These are here referred to as X3-triangles (i.e. 'times 3'-triangles).
Those triangles whose midpoints are also triangular. These are here referred to as MP-triangles (i.e. 'midpoint-triangles').
[Note: those unfamiliar with the concept of midpoint may care to link here.]
Those sequences of 3 in the general series which, when summed, yield a triangle. Their collective outcomes are here referred to as S3-Triangles (i.e. 'the sum of 3'-triangles.
4. The subsets in detail
The R-triangles
In the following tables, i and j are the order numbers of T - the associated triangles. At (a), we have the palindromic set of 23 entries, of which 3 involve digit repetition.
Of the 23 non-palindromic instances at (b), 7 only (green) are seen to be 'each-way' reversals; the remaining 16 (mauve) are not - this because in these instances the number representing the motivating triangle (column 3) ends with one or more zeros.
Thus, of the 65535 triangles represented within this range, a mere 46 (i.e. 0.07%), in one way or another, meet the criterion of reversibility. To encounter just one of these numbers in a different setting is therefore a matter of some interest.
The X2-triangles
Observe that there are only 6 instances of these triangular pairs in the whole of the range investigated.
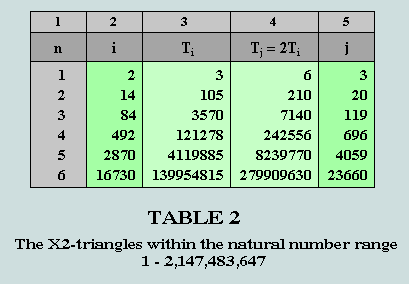
The following diagram depicts the visual implications of the triangles occupying row 2 of this table.
The X3-triangles
Table 3 records the 8 instances of these pairings that occur within the given range. Of particular interest is the fact that 210 (the 20th triangle) - which features as a multiple of 105 in Table 2 and again in Figure 4 - here appears as a sub-multiple of 630.
It turns out that this is a matter of some considerable significance.
The MP-triangles
There are just 6 instances of the phenomenon over the given range.
Observe that the midpoint triangles T(j) derive from T(i) by the simple process of adding 1 and dividing the result by 2. Clearly, this requires that T(i) be an odd number.
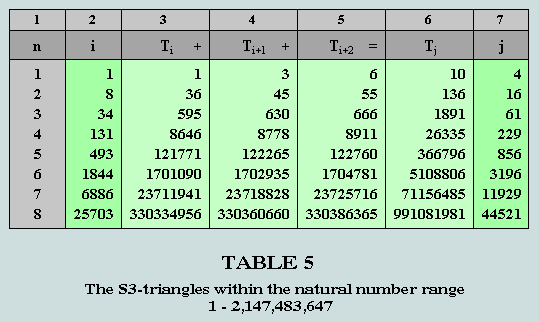
The S3-triangles
Here, we again find just 8 instances of the phenomenon over the given range. In any given row the sequence of 3 triangles involved is found in columns 3, 4 and 5, and their sum in column 6.
5. A significant confluence
An examination of the foregoing material reveals that row 3 of Table 5 is a place where a number of interesting features from the earlier tables converge, for consider:

Already, it becomes clear that 105 and its double, 210, are major players in these proceedings - and this is further confirmed by the fact that the sum of the order numbers of the triangle sequence 595, 630 and 666, viz 34 + 35 + 36 = 105.
[Note: in this same connection we observe that, whilst 35 (the order number of 630) multipled by 3 = 105, 630 divided by 3 = 210]
But, to continue the catalogue of interesting features found in row 3 of Table 5:
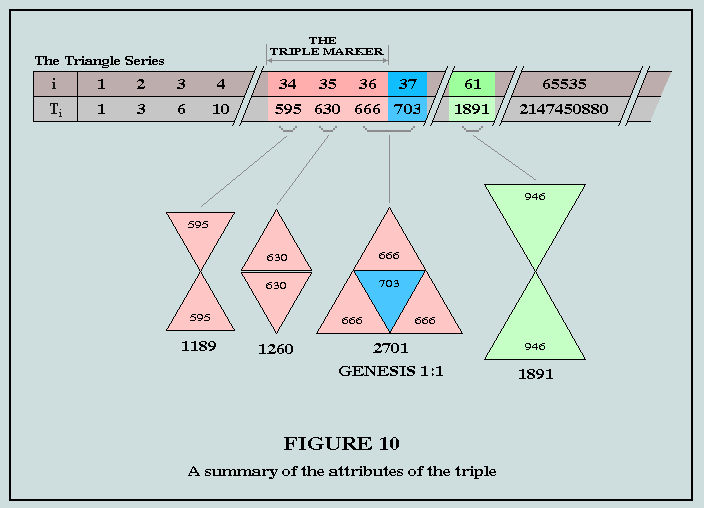
(6) On the basis of (5) above, 1891 may take the form of a symmetrical hour-glass figure, representing the fusion of two of its mid-point triangles - this structure depicted at (b) in Figure 5:
(7) The hexagon representing the self-intersection of 1891-as-triangle clearly comprises 6.210 + 1, or 1261 counters; but the self-union of the mid-point triangle, 946, also has 12.105 + 1, or 1261 counters. This phenomenon of hexagon (X) being equal to hexagram (Y) is the outcome of T(1) = 2T(2), and is quite rare (see Table 2).
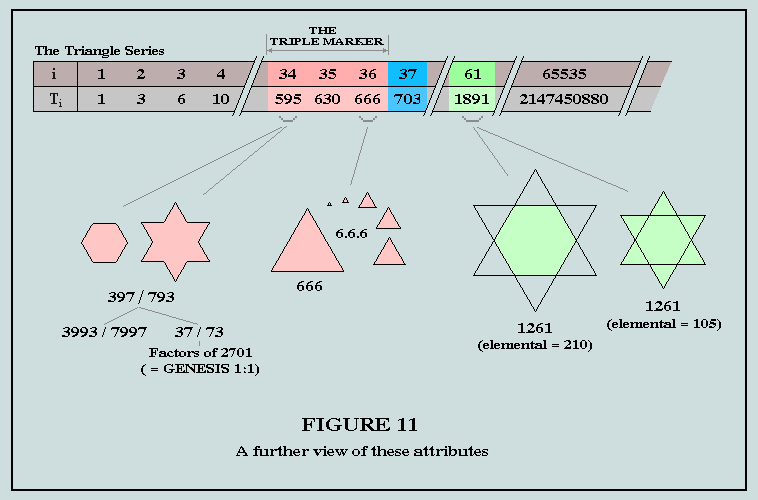
A more familiar example of the phenomenon has been aired in earlier pages, viz 37, which has a geometrical presence both as hexagon and hexagram, thus:
(8) 595 is a G-triangle (elemental = 66), and generator for the reflective hexagon/hexagram pair 397/793. This particular phenomenon of reflection in X and Y is encountered only 3 times over the range of numbers investigated - and probably, never more. It arises when the elemental of a G-triangle is 6, 66 (the present case), and 666.
This evidence is presented in Figure 8, below:
Triangle (a) comprises 595 counters; its elemental, 66, is shown at (b), and the manner in which this participates in the structure of triangle and derivatives follows in (c) and (d).
Again, 595 is the midpoint of 1189 (this number, interestingly, a cyclic permutation of 1891!) It therefore participates in an hour-glass construction with itself - the result, 1189.
(9) 630 is a simple multiple of the related triangles, 105 and 210; further, it is precisely half of 1260. As we have seen, 1261 (1 more than 1260) is a bifigurate number (X = Y) involving the elementals 210 and 105.
(10) A visually-interesting denary object, 666 is a simple repetition of the first perfect number, 6; it is a multiple of 37 - itself a singular figurate number; further, expressed as a triangle, it is unique in that all its numerical attributes are triangles, thus:

[Observe that the sum of these attributes, remarkably, = 216, or 6.6.6]
6. The scriptural mappings
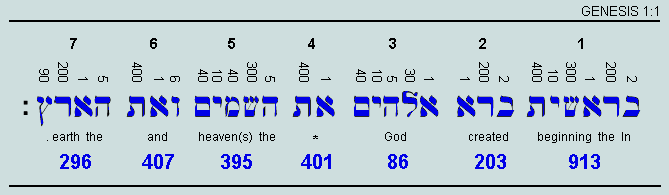
(1) What is so significant about these matters is that the triangular sequence, 595, 630, 666 is immediately followed by 703 (=19.37) - the product of X and Y in Figure 2, and the characteristic value (CV) of "and the earth." - represented by the two final Hebrew words of Genesis 1:1. [Further details here.]
(2) In view of the proximity of 666 and 1260 in the Book of Revelation, it is remarkable that 630 (one half of 1260) and 666 should be both triangles and immediate neighbours. And that 666-as-triangle has an outline of 105, i.e. one twelfth of 1260!
[Note: details of the role of 1260 in the Books of Daniel and Revelation are provided here.]
(3) The basis of the data in the following Table is set out here.
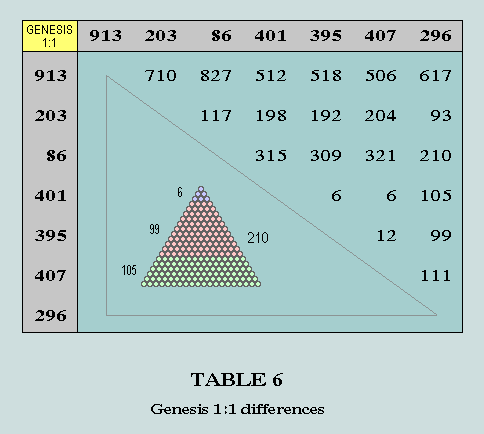
The figures in this table represent the positive differences between the numbers heading the relevant row and column. Thus, 309 (occupying the 5th column of the 3rd row) has been obtained by subtracting 86 from 395. Observe that the 15 differences that do not involve 913 are all simple derivatives of the 3 related triangular numbers 6, 105 and 210. Thus,
117 = 105 + 2.6; 198 = 210 - 2.6; 192 = 210 - 3.6; 204 = 210 - 6; 93 = 105 - 2.6
315 = 210 + 105; 309 = 315 - 6; 321 = 315 + 6; 99 = 105 - 6; 111 = 105 + 6;
and that those in which 913 plays a part follow the same scheme - provided each is first reduced by 500. Thus,
210; 327 = 315 + 2.6; 12; 18; 6; 117 = 105 + 2.6
Observe that the 3 triangles represented comprise 1st perfect number and the related pair, 105/210 - which also feature in other ways in this analysis.
These data feature also in the metric dimensions of a modern artefact - the A4 sheet of cut paper. [The details may be found here.]
(4) Concerning 37, 397, 3997: the other two cases yield 37/73 (factors of Genesis 1:1) and 3997/7993.
(5) 595 is the midpoint of 1189 which is the total number of chapters in the Bible. The 595th is Psalm 117 - a paean of praise to the Lord!
(6) 666 and its immediate neighbour 703 participate in a partitioned view of the structure of the Bible's first verse. [The details may be found here.]
(7) 1891, its midpoint (946) and 1261-as-hexagram feature in an analysis of the breastplate data (Ex.28:15-21). [The details may be found here.]
7. A summary of the findings
In Figures 10 and 11, attention is drawn to the essential mappings between the absolute truths derived from the Book of Number and, by implication, those found in God's Inspired Word - the Judeo-Christian Scriptures.
8. Concluding remarks
The sequence of 3 triangles, 595, 630, 666, has been dubbed the TRIPLE MARKER for the reason that it functions as a beacon, drawing attention to the 37th triangle, 703, representing the earth and its inhabitants, and linking with 666 in defining the whole of the first verse. A further independent link with Genesis 1:1 arises from the activities of the X2-triangular pair, 105/210 which are involved in the differences of the 7 Hebrew word-values. But there is yet another independent link with the prologue: the 397/793 phenomenon draws attention to its earlier manifestation, 37/73 - the reflective factors of 2701, its characteristic value.
Then, again, we have the matter of the two intriguing numerical representatives of the Book of Revelation, 1260 and 666. Why should we find these scriptural companions related also by the TRIPLE MARKER? And what of the significance of the day following the 1260th - this day singularly marked by a bifigurate number?
Finally, why should the central chapter of the Bible be the 595th; and why should this (Psalm 117) be the shortest chapter - taking the form of a paean of praise to the Lord? A moment's thought should convince any thinking person that there are too many coincidences here for comfort! Will we yet again take cover by invoking a miracle of chance? Or will we yield to reality and logic and begin to learn something new about the Judeo-Christian Scriptures - ever mindful of the Lord's promise of wisdom to those prepared to follow this course.
And, by the way, those who, despite the clear directive of Rev13:18, question the legitimacy of reading Hebrew and Greek words as numbers should consider that neither the data relating to 1260 and 666, nor to the Bible's central chapter, are obtained in this way. It is only the reading of Genesis 1:1 that is; and since all these evidences are in general agreement, all must be equally valid.
Can there be any doubt therefore that - however imperfectly - we here outline thoughts that must have crossed the Mind of the Creator Himself as He sought to devise a long-term strategy for the safeguarding of the integrity of His Word in a time of gross apostasy and unbelief - in short, a time such as ours?
Vernon Jenkins MSc
2006-06-05
Acknowledgement: The author is extremely grateful to Stephen Espenschied who first brought this important matter to his attention.
email: vernon.jenkins@virgin.net
ADDENDUM: FURTHER EVIDENCES OF TRIPLE MARKING
The 'triple marker' theme is repeated thrice more. First, in connection with 10 - principal radix and collective unit of man's systems of numeration and measurement; then, in respect of 'Elohim' - the Creator's Name - as we find it recorded in the Hebrew of the Bible's opening verse; and finally, in a direct relationship with Genesis 1:1 and the opening terms of the hexagram series of numerical geometries.
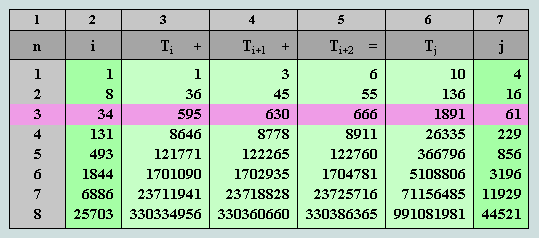
To develop these observations it is necessary that we begin by reviewing the S3-Triangles (as set out in Table 5 above), i.e. those sequences of 3 consecutive terms drawn from the general triangle series whose sum is also triangular. For convenience, a copy of this table is provided below with the original triple marker highlighted.
The unique significance of ten
In an earlier page, A matter of numerical symbiosis, it was argued that ten and the denary system of numeration are divinely-ordained absolutes in the world of number. This conclusion appears to be borne out in the first row of this sparse subset of the triangular numbers where the sum of the first 3 terms of this infinite series is found to be 10.
The Elohim phenomenon
The Hebrew word 'Elohim' (pronounced 'Eloheem' and traditionally translated 'God' - though it is actually the plural form of 'Eloah'!) is first encountered biblically as the third word of Genesis 1:1 (reading from right to left in the traditional manner):
Note that 'Elohim' has five letters whose values as numerals are 1, 30, 5, 10 and 40, respectively.
[Those unfamiliar with the Hebrew scheme of numbering kindly click here]
This name for God occurs 228 times in the Torah (or Pentateuch). A few years ago the researcher, Ian Mallett, drew attention to the interesting fact that if the letters of this name are read as three groups of three - that is, 1st/2nd/3rd, 2nd/3rd/4th and 3rd/4th/5th - the corresponding CVs (obtained by summing the constituent numerals) are 36, 45 and 55, ie a rising sequence of consecutive triangular numbers (the 8th, 9th and 10th). These facts are detailed in the following panel:
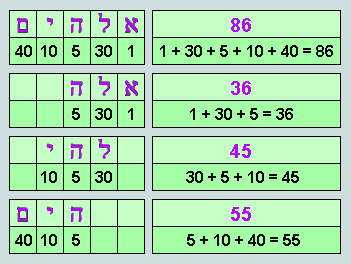
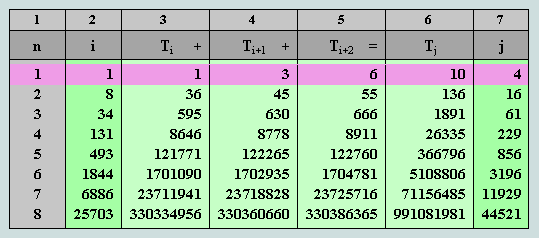
Observe that the sum of these three triangles is 136 (16th triangular number) and the sum of their order numbers, 8 + 9 + 10 = 27 (the cube of 3). Significantly, these numbers are found to occupy the second row of the S3 table and clearly represent a third triple marker!
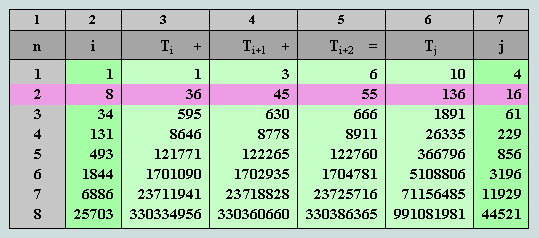
At this point it is appropriate that we pause to consider the true significance of these facts, for it is not evident that in a language based on an alphabet of 22 letters, a name of 5 letters is likely to have such a special numerical property.
A formal analysis reveals that the number of unique strings of 5 Hebrew letters is 5,153,632 (i.e. 22 x 22 x 22 x 22 x 22) - of which 42 only display a rising sequence of consecutive triangles. These are detailed in the following table.
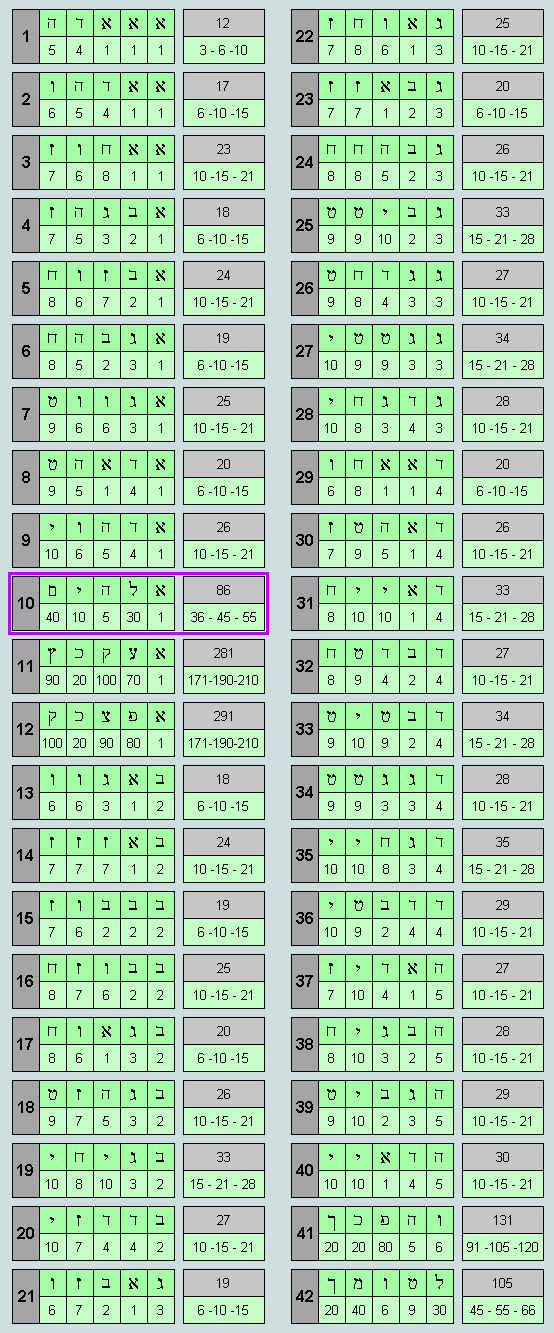
Note that these 5-letter Hebrew 'names' together with their associated letter-values are to be read from right to left; the resulting 3-triangle sequence that appears below the name CV is to be read in the usual manner.
Observe, (1) that the elohim instance occurs, appropriately, as the 10th in this sequence, (2) that it alone represents a valid Hebrew word, (3) that it alone yields the sequence 36-45-55 which is found in S3 and, (4) that this sequence alone yields a sum which is also triangular, viz 136 - the 16th of the series. Thus, the probability that this name was chosen in ignorance of its profound numerical implications is vanishingly small. Yet it is also clear that the Hebrew scheme of alphabetic numeration post-dated the writing of Genesis 1:1 by many centuries!!
Finally, under this heading, consider the fact that three - the first triangular number proper - is a persistent feature of these proceedings, thus:
The factors of Genesis 1:1 viz, 37 and 73, are revealed as hexagon and hexagram, respectively, when the third of the elohim triangles, 55 (incidentally, symbolizing a pair of human hands!) is symmetrically united with an inverted copy of itself.
its plural form lends support to the Christian doctrine of the Trinity.
having 5 letters, there are just three successive groups of three adjacent letters
each group of 3 yields a triangle
these triangles are in rising ordered sequence
the sum of these 3 triangles yields another - 136
this sum - as a denary (or base 10) number - has three digits which reveal the first three triangular numbers (1, 3 and 6)
again, the digit sums are interesting: 1+3+6 = 10 (triangular); (3+6)+(4+5)+(5+5) = 28 (triangular); 2+8 = 10, and 1+0 = 1 (first, and degenerate, member of the triangular series)
other radix-dependent features of interest include: (a) with 'elohim', the first word of Genesis 1:1 forms 999 and, (b) with two other nouns 'heaven' and 'earth', it forms 777; these three-digit eye-catchers are multiples of 111, or 3 x 37
finally, as already noted, three is itself triangular!
The star of stars of stars
We conclude this addendum by drawing attention to yet another weighty feature of S3 - this tiny subset of the triangular numbers. It again concerns Table 5 - reproduced here, for convenience, with the 4th row highlighted.
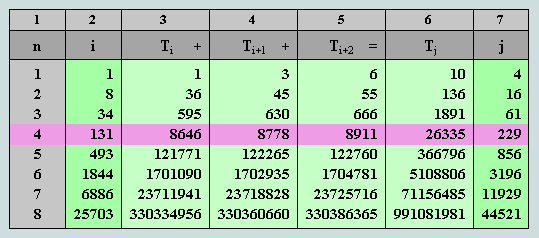
Here we observe the sum of the triangular triple, 8646, 8778 and 8911 to be 26335 - the 229th in the general series of triangles, and 77th G-triangle. The derivatives of this triangle by self-intersection / union are 17557 / 35113 - 77th hexagon and hexagram, respectively. Observe that the latter factorises thus: 35113 = 13 x 37 x 73, i.e. the product of the 2nd, 3rd and 4th terms of the numerical hexagram series - and hence, itself, a triple marker of a higher order!
A reading of Genesis 1:1 - based upon the Hebrew scheme of alphabetic numeration - reveals it to be the large triangular number 2701, or 37 x 73, i.e. product of the 3rd and 4th numerical hexagrams. Furthermore, we observe that within this verse the sum of the words representing 'God' and 'heaven' is 481, or 13 x 37, i.e. the product of the 2nd and 3rd numerical hexagrams. It therefore follows - most remarkably - that the hexagram derived from the 4th triple marker may be realised as a star of stars of stars - as established below.
First, we consider the regular structure of 481 as a star of stars:

Then, using this figure as a structural unit, we construct the following hexagram of 73:

This star of stars of stars clearly incorporates 13 x 37 x 73, or 35113 counters - its compound symmetries a visual expression of an important derivative of the 4th triple marker.
Vernon Jenkins MSc
2006-07-10