THE GREAT A4 MYSTERY
A facet of the Genesis 1:1 miracle
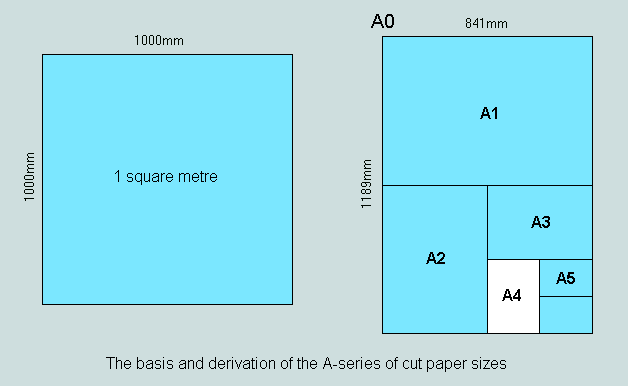
Recommended as an international standard by ISO in 1961, the A-series of cut paper sizes is now well-established in many countries. It is based upon a rectangle (A0) having an area of one square metre and sides in the ratio 'square-root of two to one'. These proportions are automatically conferred upon its progeny - A1, A2, A3, and so on - by the simple process of halving. All dimensions are expressed to the nearest whole number of millimetres.

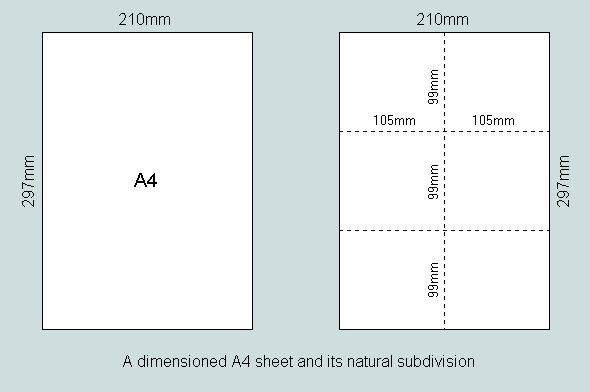
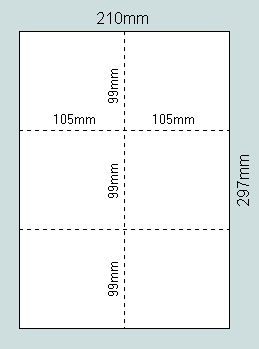
Its best-known representative is A4 - currently the most popular medium for recording and communicating the written word. This is nominally 297mm x 210mm and represents an area of one sixteenth of a square metre. It may be subdivided into 6 equal parts - each of dimension 105mm x 99mm.
Here is the set of eight numbers that represent a fair alternative reading of the Hebrew of the Bible's opening verse (of 7 words) and next following word:
G = { 913, 203, 86, 401, 395, 407, 296, 302 }
[Details concerning the derivation of this number set may be found here]
That these numbers are found to be simple derivatives of the metric dimensions of A4 is clearly a matter of some consequence - a proof requiring nothing more than access to a pair of A4 sheets and a long ruler graduated in millimetres.
However, before setting off along this path let us observe that the 7th of the set is one less than 297 (i.e. the length of an A4 sheet in millimetres), and that the 3rd is one less than 87 - the difference (in millimetres) between its sides. Undoubtedly, an interesting preface to what follows!
Operations based on the 1000mm mark
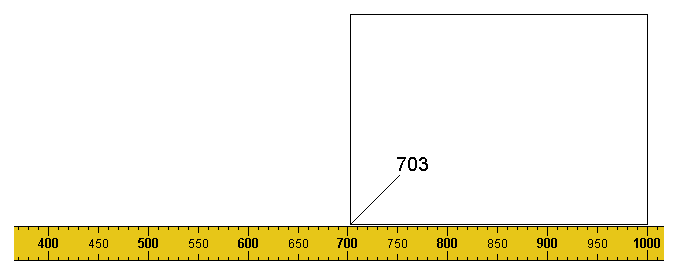
Here, observe that the right-hand edge of one of the A4 sheets has been aligned with the 1000mm graduation of the ruler - the left-hand edge then falling on 703 (i.e. 1000 - 297 = 703). Reference to the G-set above reveals the fact that 401+302 (4th + 8th) = 407+296 (6th + 7th) = 703.
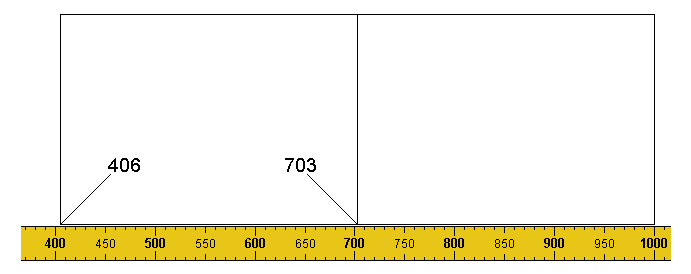
This graphic - an extension of the first - shows a second A4 sheet tightly abutted against the first. Its left-hand edge falls on 406 (i.e 1000 - 297 - 297). Note that 406 is double 203 - the 2nd of the foregoing set.
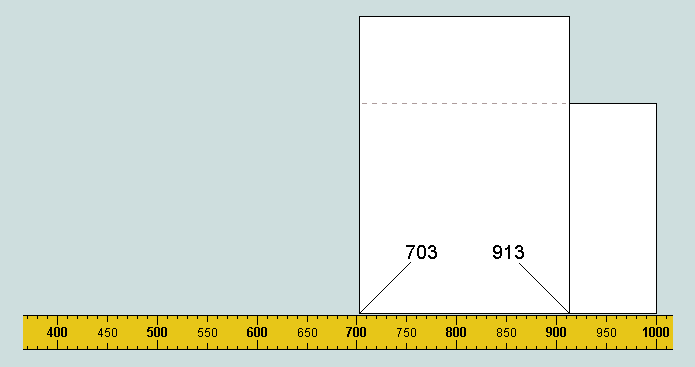
Here the second sheet is shown turned on its end - its left-hand edge aligned with the left-hand edge of the first. Observe that its right-hand edge lies at 913 - the 1st of the set (i.e. 1000 - 297 + 210 = 913).
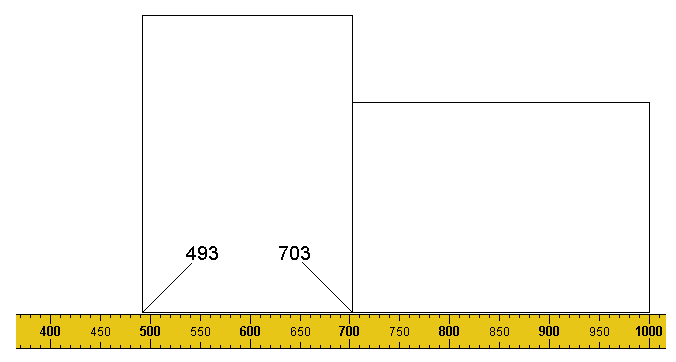
Abutted against the left-hand edge of the first sheet, the left-hand edge of the second falls on 493 (i.e 100 - 297 - 210). This represents the sum of 3rd + 7th (i.e. 86+407).
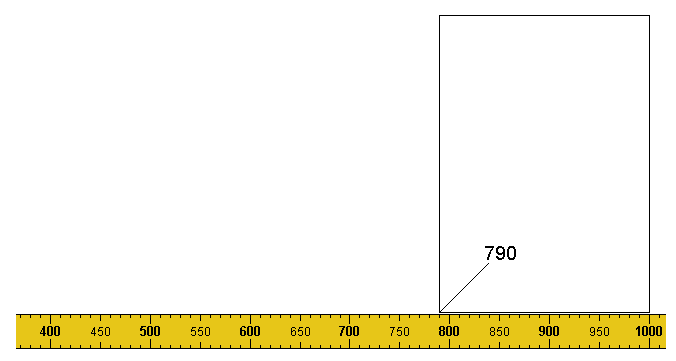
Finally, in this sequence, the first A4 sheet is removed and the second is moved along until its right-hand edge lies on the 1000mm graduation. Its left-hand edge is then seen to lie on 790 (i.e. 1000 - 210 = 790) - double the 5th of the set.
These five simple maneovres have therefore uncovered all eight of the extended Genesis 1:1 set as paired values - except for the first.
Operations based on the 500mm mark
The following procedures - centred on the 500mm mark - all involve the use of segmented A4 sheets, i.e.
Here is the first which, remarkably, generates 3 members of the set, precisely:
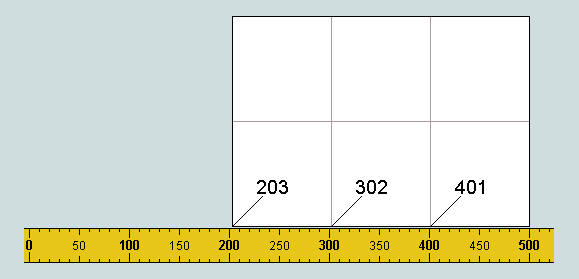
203, 302 and 401 are, respectively, 2nd, 8th and 4th of the set.
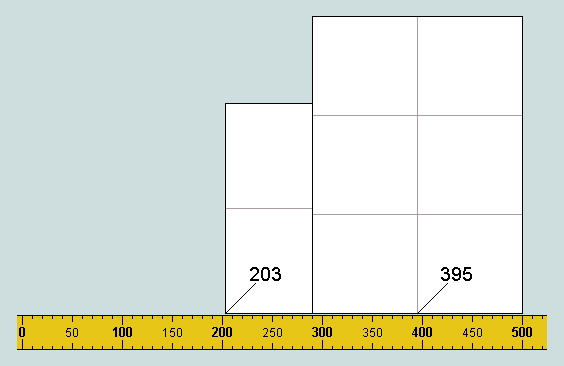
Here we generate 395 - the 5th value.
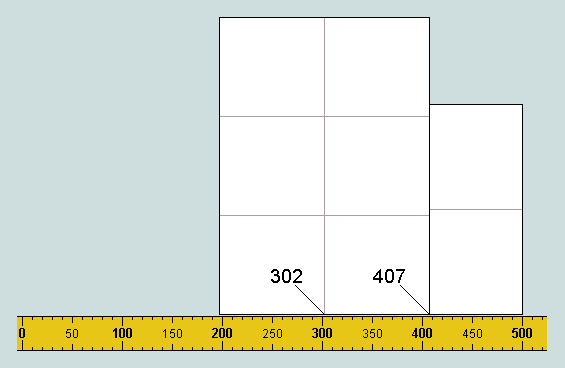
Moving the second sheet so that its central vertical coincides with the 302 discovered by the first reveals 407 (the 6th of the set) at its right-hand edge.
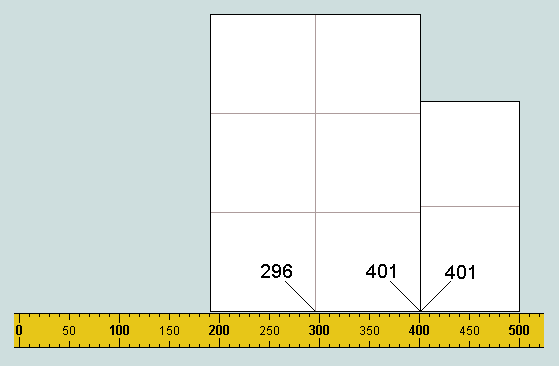
Again, moving the second (upper) sheet leftward so that its right-hand edge lies on the 401 discovered by the first reveals 296 (the 7th of the set) at the central vertical.
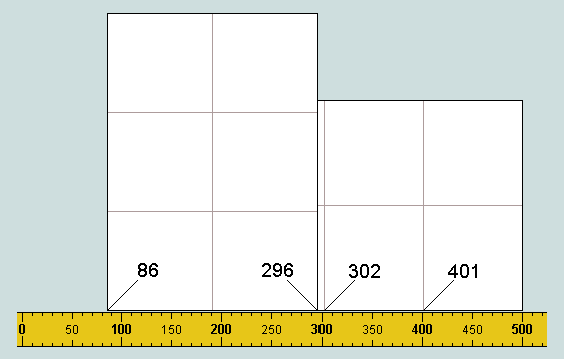
Finally, moving the right-hand edge of the same sheet onto the 296 just discovered reveals 86 (the 3rd of the set) at its left-hand edge.
Thus all values except the first, 913, have been generated by this last series of maneouvres. However, this number was identified earlier as the only single value arising from manipulations involving the unsegmented sheet. Thus, the whole of the G-set has been derived simply from operations involving nothing more than two A4 sheets and a long ruler graduated in millimetres!
And one final observation: the A-series, and A4 in particular, is defined in the document headed ISO 216. Now 216 is the cube of 6 which happens to be the outline of the Genesis 1:1 triangle. In the context of our discussion, therefore, this sequence number could not be more appropriate!
Vernon Jenkins MSc
2004-06-10