Appendix 4 - An Introduction to Numerical Geometry
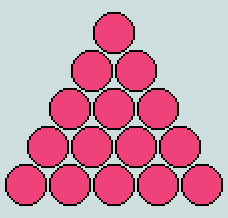
Mathematics is universally respected as a primary source of objective truth - hence its distinguished appellation Queen of the Sciences. In essence it is concerned with number and form - concepts that are found uniquely combined in a particular class of objects: the figurate numbers. The simplest of these arises directly from the operation of counting by reciting the sequence of natural numbers thus: "One, one plus two, one plus two plus three, ...", so generating the series (or sequence) of triangular numbers - 1, 3, 6, ..., without limit. A typical instance is seen in the game of snooker where the 15 'reds' are arranged in close equilateral triangle formation at the beginning of each frame. Here is a depiction of this triangle:

Clearly, the threefold symmetry of form exemplified here is a fundamental property of 15 - one that is completely independent of any other symbolism that might be invented to represent this number, and one that is direct, universal and immutable.
Two classes of the figurate numbers may be recognised, viz plane and solid - being the number of uniform counters (i.e. circles or squares, spheres or cubes, as appropriate) that would completely fill a regular polygonal or polyhedral envelope. These classes comprise a variety of symmetrical forms - each represented, (a) by the terms of an infinite series and, (b) by a characteristic formula which - given its position in the series - evaluates a selected term.
Numerical geometry is that branch of mathematics concerned with the study of such entities.
Some examples:
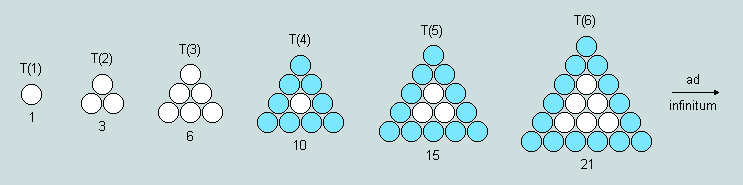
(1) Here are the opening terms of the plane series of triangular numbers:
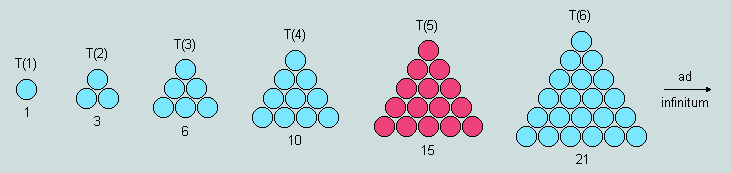
Observe that the first term - represented by a single counter - is common to all series, whether plane or solid (it is said to be degenerate because it offers no clue as to the subsequent developments). Here, it is followed by the second (2 more than the first), the third (3 more than the second), the fourth (4 more than the third), and so on - these appearing as successive rows in the growing structure. Each term is uniquely designated by the number of counters forming a side. Thus the 'snooker' triangle (occupying the 5th position in the series) may be conveniently designated T(5). Interestingly, T(4) is the tetraktys of the ancient Greeks.
Such figures have 3 axes of symmetry. In general, T(n) = the sum of the numbers named when counting to n. Thus, for example, T(9) - the 9th triangular number = 1+2+3+4+5+6+7+8+9 = 45. Alternatively, T(n) = n(n+1)/2 = 9x10/2 = 45, as before.
The triangle series is fundamental to the study of numerical geometry because, ultimately, all other figurate series are derived from it.
(2) The sum of any two adjacent terms of the triangle series yields a rhombus. This is demonstrated in the rhombus series depicted below.
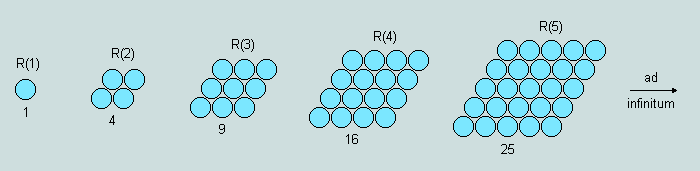
As may be observed, a rhombus possesses 2 axes of symmetry.
(3) The more familiar square series is derived from the latter by a simple adjustment of the counter packing arrangement - accompanied, maybe, by a more appropriate choice of counter shape, thus:
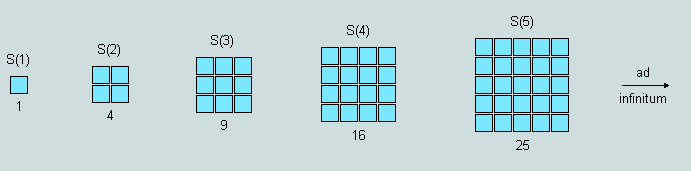
Squares posses 4 axes of symmetry with S(n) = R(n) = n^2.
[Observe here the use of the uparrow (^) to signify 'to the power of'.]
(4) Another form capable of completely filling a square frame is the diamond.
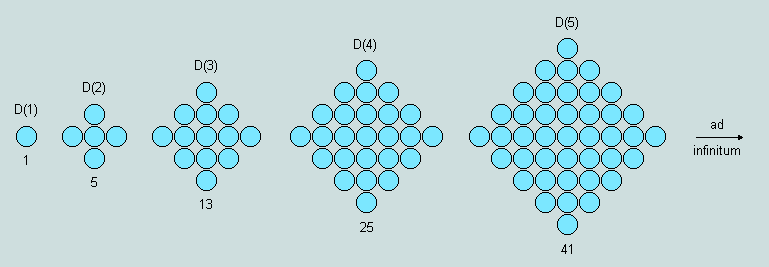
The number of counters forming each of these structures is obtained by doubling the product, n(n-1), and adding 1. Thus, D(n) = 2n(n-1) + 1.
(5) A given numerical triangle may be united with an inverted copy of itself to create a structure that has the form of an hour-glass. Here are the opening terms of this series:
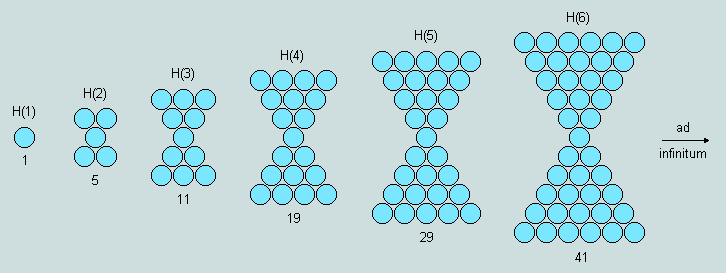
Such figures possess 2 axes of symmetry with H(n) = n(n+1) -1
(6) The symmetrical truncation of every third term of the square series results in a sequence of octagons, each of which has 4 axes of symmetry, thus:
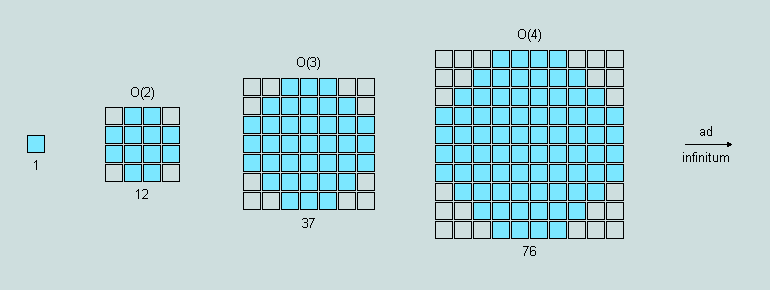
The characteristic formula here is O(n) = 7n^2 - 10n + 4
(7) Before introducing the hexagon and hexagram series (each possessing 6 axes of symmetry) it is necessary that we first develop a broader understanding of the triangle series.
Based upon the nature of its geometrical structure a triangular number may be classified under one of three headings , viz 1-centre, 3-centre or 6-centre, depending whether it is built around the 1st, 2nd or 3rd terms of the series. The following diagrams explain the principle:
Observe that T(4) - and every 3rd term thereafter - has a single central counter; T(5) - and every 3rd term thereafter - has a central group of 3; and T(6) - and every 3rd term thereafter - has a central group of 6. Clearly, proceeding from one term to the next higher in the general series simply involves the addition of a further row of counters, whereas proceeding to the next higher in any of the 3 groups requires the addition of a complete ring of counters.
The 1-centre triangles - as defined in the previous section - may be aptly termed generator triangles for the simple reason that each is capable of generating a symmetrical hexagon/hexagram pair by self-intersection/union about the central counter. Here are the early terms of the generator triangle series:
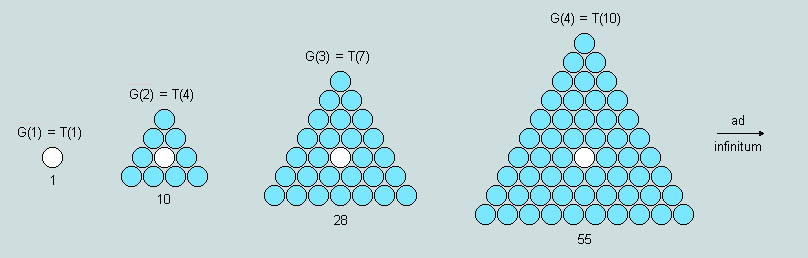
Again, observe that the first term of the series is degenerate. The first 3 generator triangles proper are therefore G(2), G(3) and G(4) - corresponding to T(4), T(7) and T(10), respectively. Clearly, the order of a G-triangle - as thus defined - is equal to the number of rings of counters surrounding the central counter plus 1.
As the following diagrams reveal, every G-triangle proper may be envisaged as comprising 9 congruent elemental triangles (drawn from the general series) set symmetrically about the central counter. Two colours have been used to make the principle clear.
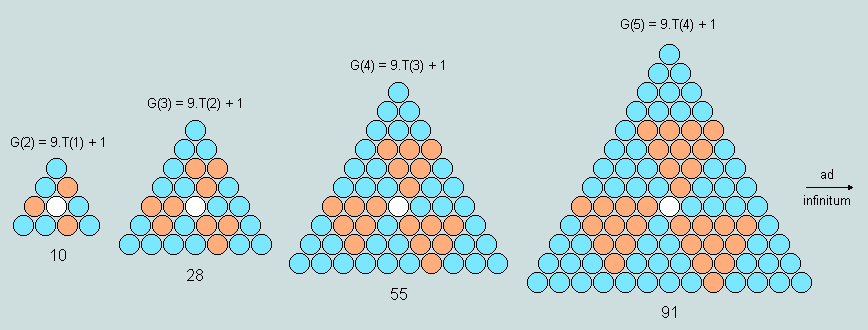
It is this feature that allows any G-triangle to function as the generator of a symmetrical hexagon/hexagram pair (X/Y) by self-intersection/union, as the following example shows.
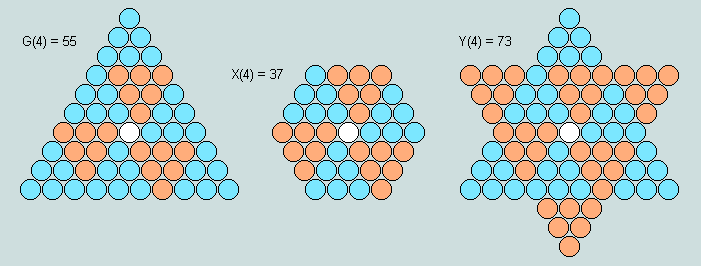
Observe here that
as with G, the order number of the X/Y pair is one more than that of the elemental triangle involved in their structures; thus, in the above example, the 4th X/Y pair involve the 3rd triangle of the general series
the number of elemental triangles in X is 6, and the number in Y is 12
It therefore follows that, if n be the order of the elemental triangle,
- G(n+1) = 9n(n+1)/2 + 1
X(n+1) = 6n(n+1)/2 + 1
Y(n+1) = 12n(n+1)/2 + 1
(8) Some simple examples of figurate solids are cube, tetrahedron and pyramid.
These comprise stacks of unit cubes or spheres - each form being associated with its own infinite series. Thus the tetrahedron may be envisaged as a stack of consecutive triangular numbers; and the pyramid as a stack of consecutive squares. The perfection of shape is here expressed in terms of planes of symmetry - the cube having 9, the tetrahedron 4, and the pyramid 6. The characteristic formulae associated with these are as follows:
Cube: C(n) = n^3
Tetrahedron: Q(n) = n(n+1)(n+2) / 6
Pyramid: P(n) = n(n+1)(2n+1) / 6
Associated with the study of these entities is the concept of polyfiguracy. In other words, certain whole number may be expressed visually as a symmetrical arrangement of counters in more ways than one. Thus, D(4) = S(5) = 25; S(8) = C(4) = 64; X(3) = H(4) = 19; and so on. Such numbers are said to be bifigurate. Just two are observed to be trifigurate; they are 37 and 91.
Thus, Y(3) = X(4) = O(3) = 37:

and P(6) = X(6) = T(13) = 91:
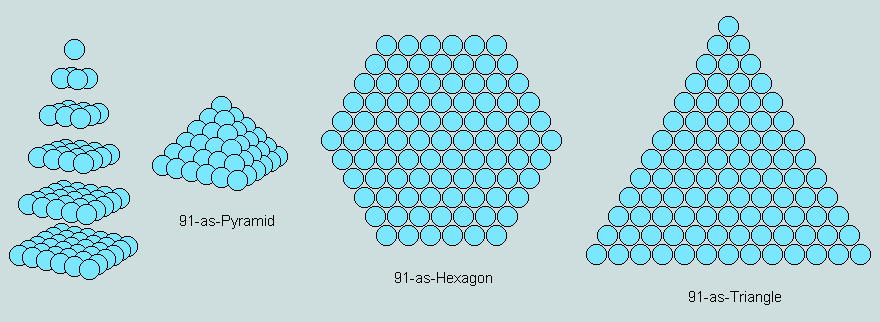
Within the parameters defined, the author is not aware of instances involving a higher order of figuracy.
In general, it can be said of the figurate numbers that such self-evident associations of number and form represent precious and irrefutable outcrops of absolute truth in a confused world.
Vernon Jenkins MSc
2006-01-30