An introduction to the triangular numbers

General principles

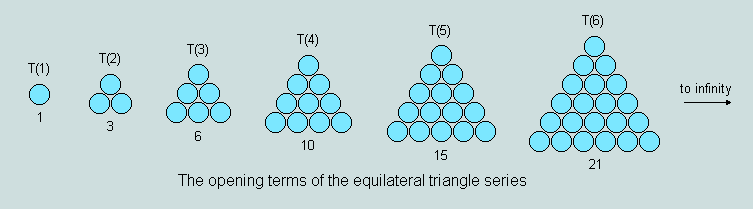
The triangular numbers represent an important subset of the infinite set of positive integers (alternatively known as natural, whole or counting numbers). A triangular number (here designated 'T') is so called because, when expressed as a group of uniform circular counters, it is capable of filling completely a frame having the form of an equilateral triangle. The following diagrams explain the principle.

Such numbers are simple derivatives of the natural numbers and of the counting process, "one, two, three, ..." where, instead, we say, "one, one plus two, one plus two plus three, ...". This is evidenced in the structure of each triangle. Each term in the series is uniquely identified by a number representing its ordinal position - this matching the number of counters forming a side of the related triangle.

Given the order (i, say) of a triangular number, its value may be calculated in one of two ways - either, (a) by adding together the numbers named when counting to i, or (b) by forming the product i(i+1) and halving the result. To illustrate these alternative procedures, let us suppose we need to calculate (1) the 7th term T(7), and (2) the 37th term T(37) of the series.

(1) Using (a): 1+2+3+4+5+6+7 = 28; using (b): 7 x 8 / 2 = 28

(2) Using (a): 1+2+3+4+...+35+36+37 = 703; using (b): 37 x 38 / 2 = 703.

Based upon the nature of its geometrical structure a triangular number may be classified under one of three headings , viz 1-centre, 3-centre and 6-centre, depending whether it is built around the 1st, 2nd or 3rd terms of the series. The following diagrams explain the principle:

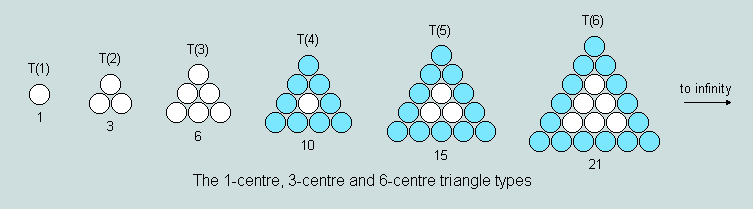
Observe that T(4) - and every 3rd term thereafter - has a single central counter; T(5) - and every 3rd term thereafter - has a central group of 3; and T(6) - and every 3rd term thereafter - has a central group of 6. Clearly, proceeding from one term to the next higher in the general series simply involves the addition of a further row of counters, whereas proceeding to the next higher in any of the 3 groups requires the addition of a complete ring of counters.

The generator triangles (G)

The 1-centre triangles - as defined in the previous section - may be aptly termed generator triangles for the simple reason that each is capable of generating a symmetrical hexagon/hexagram pair by self-intersection/union about the central counter. This subset of the triangular numbers is also distinguished, (a) by the presence of all perfect numbers except 6 (the first) and, (b) as normally expressed in base 10 (ie denary or decimal) notation, the digits of each term after the first sum, penultimately, to 10. [Details of this matter may be found here.]

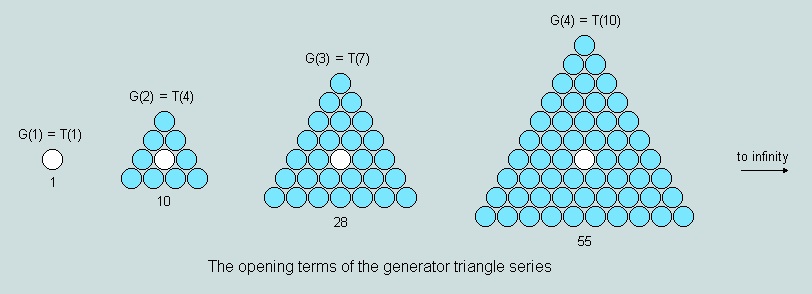
Observe that the first term of the series is degenerate, but is, nevertheless, designated G(1). The first generator triangle proper, G(2), is 10, the second 28, and the third 55 - corresponding to T(4), T(7) and T(10), respectively. Clearly, the order of a G-triangle is equal to the number of rings of counters surrounding the central counter plus 1. This principle becomes apparent when successive rings are displayed in different colours, as in the next diagram.

Based on the foregoing diagram a number of self-evident features of G-triangles follow, viz

Additional properties are revealed by following a different train of thought. As the following diagrams reveal, every G-triangle may be envisaged as comprising 9 congruent elemental triangles (drawn from the general series) set symmetrically about the central counter. Two colours have been used to make the principle clear.

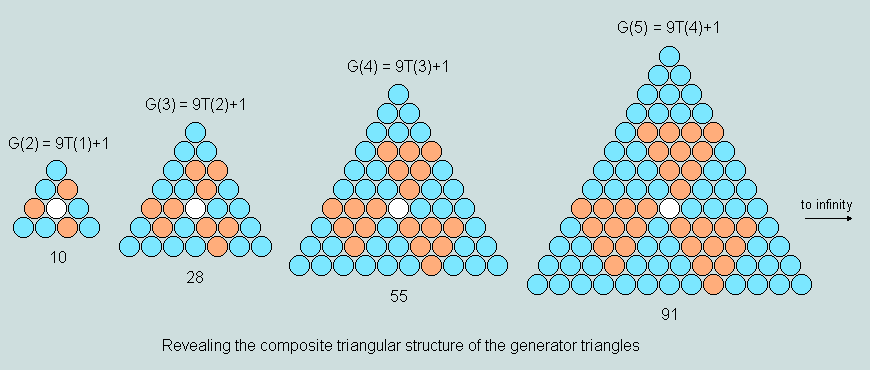
It is this feature that allows any G-triangle to function as the generator of a symmetrical hexagon/hexagram pair (X/Y) by self-intersection/union, as the following example shows.

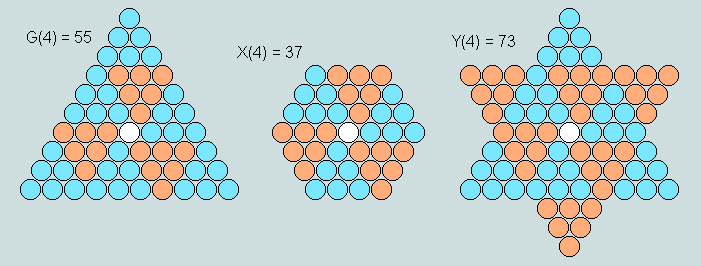
Observe here that

 

Vernon Jenkins MSc

2003-08-08