

5 - THE TRUE SIGNIFICANCE OF TEN REVEALED
1 - Introduction
This page (formerly titled 'Numerical Symbiosis') documents reasons for believing ten and the denary system of numeration to be absolute, and divinely ordained. In many of the arguments presented, three and six appear as close companions of ten, and while the significance of three will become clearer as we proceed - chiefly in respect of the triangular geometries which underpin many of the matters discussed - six is deserving of closer inspection. It has therefore been made the subject of the opening section where its own considerable attributes, by association, do much to elevate the status of ten.
2 - The importance of being a half-dozen
2.2 - these features may be demonstrated independently of any symbolic system of numeration using 6 uniform circular counters, as shown; at (a) we have 6 as 3rd triangular number, comprising 3 rows of 1, 2 and 3 counters, while at (b) 6 is shown as a (1)x2x3 rectangle:
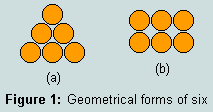
2.3 - these observations lead to an understanding of the attribute of 'perfection' in number; 6 is the first of a relatively sparse subset of the natural numbers - the perfect numbers - each of which is equal to the sum of its factors - including 1; all known examples are even and triangular; they have interested mathematicians from the earliest times
2.4 - as a triangular number, 6 is the double of another, viz 3; there are just 6 instances of this phenomenon in the first billion natural numbers, and here we have the first of them
2.5 - 6 is the only known triangular number whose square, 36, is also triangular:
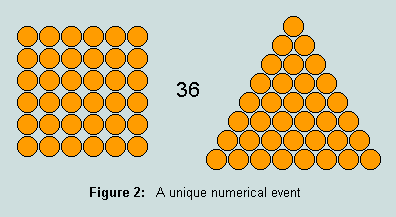
2.6 - 6 shares a symmetrical relationship with 7 - the hexagonal form of the latter (a) being reduced to 6 when the central counter is withdrawn (b):
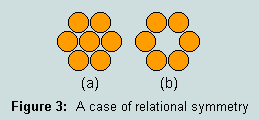
2.7 - the prime numbers represent the 'backbone' of the natural number sequence; all primes after the first two, viz 2 and 3, are of the form 6n-1 or 6n+1, n being some natural number; eg both 11 (= 6.2-1) and 13 (= 6.2+1) are prime; observe that the two exceptions are the factors of 6
2.8 - every cube or cuboid (the most common of regular solids) has six faces; this implies that a cube of dimension 6 is unique in that its superficial area is numerically equal to its volume; the same is true for a sphere of diameter 6 units
3 - First impressions of ten
3.1 - 10 is the sum of the first four natural numbers, 1, 2, 3 and 4; like six, it is therefore a triangular number, (a):
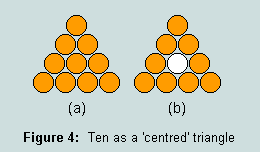
3.2 - however, unlike the triangular representation of six, this figure has a 'centroid' counter - here rendered white, (b); from this point on, every third triangle in the infinite series of triangular numbers has this representation of ten as its centre
3.3 - triangles of this kind have the ability to generate other symmetrical figures by self-union /-intersection; in particular, 13-as-hexagram and 7-as-hexagon are seen to derive from 10-as-triangle, thus:
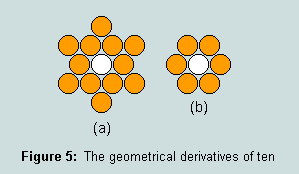
The sixness of these figures should not pass unnoticed.
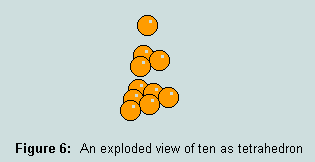
3.4 - ten may also be represented geometrically as a tetrahedron - the sum of the first three triangular numbers, 1, 3 and 6, thus:
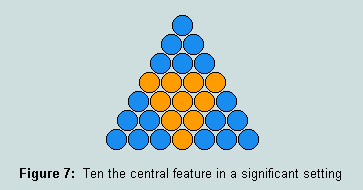
3.4 - another simple construction reveals 10 as central feature in a setting of perfect numbers, viz 6 (the first) and 28 (the second):
3.5 - from Figure 4(a), let us observe that the ratios of adjacent rows in the triangle have important musical connotations; interpreted in terms of frequencies, they specify the perfect intervals of octave (2:1), fifth (3:2) and fourth (4:3)
4 - The way we write numbers today
Our current number system is, of course, firmly based on ten as radix and uses the following set of graphic signs, often referred to as Arabic numerals: {0 1 2 3 4 5 6 7 8 9}. These are subject to the rule of position since their value depends on the place they occupy in a written numerical expression (a 7, for instance, counts as seven units, seven tens, or seven hundreds depending on its position in a three-digit numerical expression). In his comprehensive book, "The Universal History of Numbers", Georges Ifrah writes, "...the almost universal preference for base (or radix) 10 comes from nothing more obscure than the fact that we learn to count on our fingers, and that we happen to have ten of them."(p.44)* Thus, according to one's view of how things have come to be, either the ten digits appeared by chance, or they must represent the Creator's preferred choice.
* Others offer a different explanation for the primacy of ten - typically believing it to derive from the Babylonian sexagesimal system and/or the high regard for the tetraktys (the triangular form of ten) among the ancients.
5 - Reduced digit sum (RDS)
A simple but important derivative of any written denary number is obtained by summing its digits, summing the digits of the result and, if necessary, repeating the procedure until a single digit remains. We may conveniently refer to this outcome (R, say) as the RDS of the original number (N, say). It may be shown that R is equal to the remainder when N is divided by 9. As an example, suppose N = 7463230896, then r1 = 48; r2 = 12; r3 = R = 3 - where r1, r2,... represent the intermediates in this process. Observe that when R = 1, the penultimate result is equal to the system radix, namely 10.
6 - Digit patterns
The presence of digit symmetry in certain denary numerical expressions may form the basis for argument supporting the elevated status of ten - such patterns disappearing when the numbers involved are written in a different system - as, for example, binary or octal. As an example, consider the unique numerical absolute 666 - ie 600 + 60 + 6 - the repeated digit being first perfect number. As the following table reveals, the appearance of this number in other systems (radices 2 to 36, inclusive) reveals no pattern of equivalent interest:
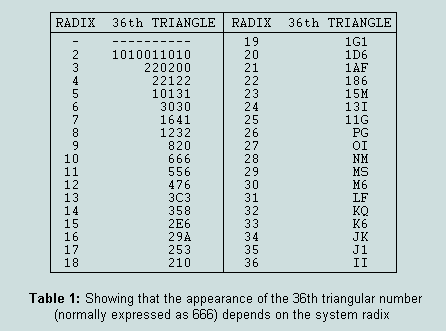
Note: Since the number of graphic symbols required is equal to the radix, it is usual to augment the standard set of ten with as many alphabetic characters as are necessary to meet the specific requirements. Table 2 details the values assigned to the 26 alphabetic characters available for use in the construction of Table 1:

7 - The remarkable geometry of 666
Six hundred and sixty-six per se may be justly described as a singularly interesting numerical absolute: it is the triangular number that stands on a base of 36 - which, as Figure 2 reveals, is the only number which is both square and triangle. It is represented here as an array of rectangular tiles:
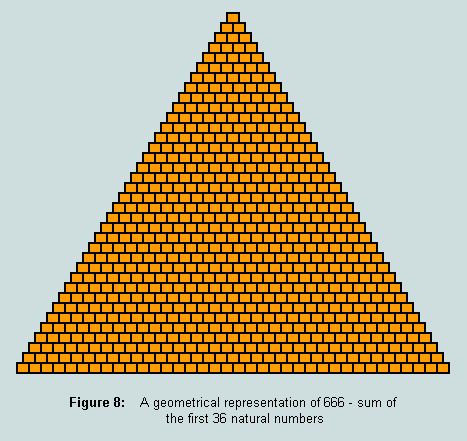
As we view this figure, let us observe its essential threeness, the number of tiles forming its base (36), and the number involved in its outline (105). Clearly, all are absolute attributes of 666-as-triangle and, significantly, all may themselves be represented as triangles:
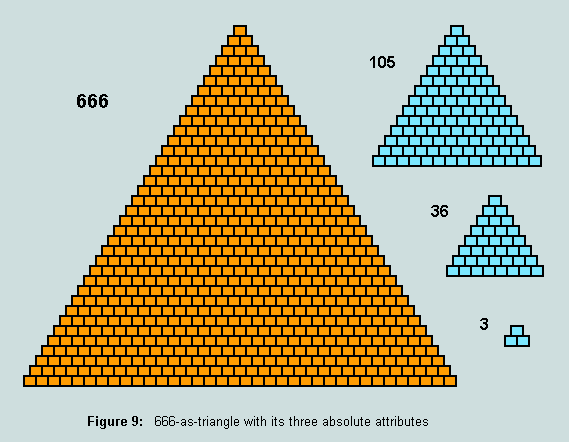
Observe that these features are numero-geometrical absolutes. In other words, they are completely independent of time, of position, and of symbolic representation (involving the concept of radix). Turning now to the way we write 666 as a denary object, two further triangles are observed, viz 6 (the repeated digit in '666' which also happens to be first perfect number), and 66 (a second number represented within the string '666'). These additions extend our understanding of this remarkable number, 'six hundred, threescore and six' (its biblical AV designation - as recorded in Rev.13:18).
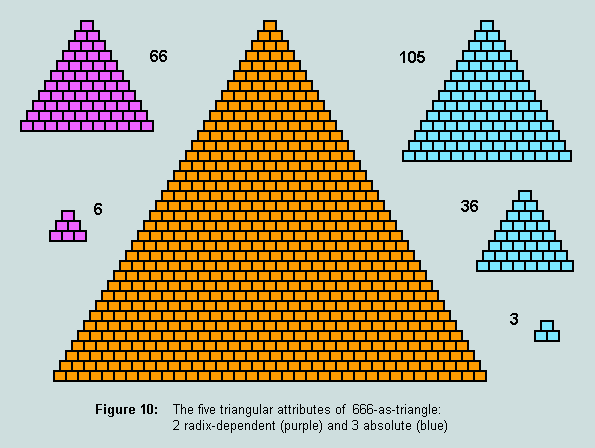
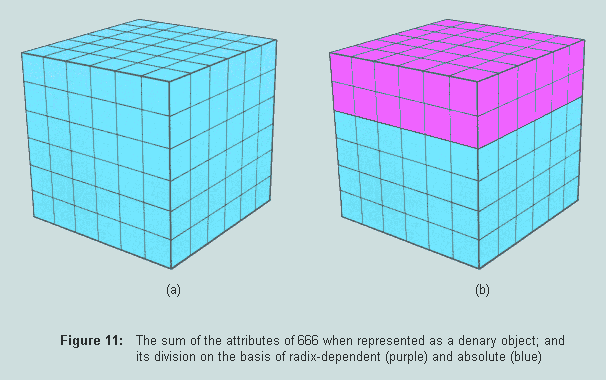
A further remarkable fact now arises: the sum total of these five attributes is 216, or 6.6.6, the cube of 6, (a). But not only that! The denary/absolute divide is 72:144, or 1:2. This fact is captured below, (b).
8 - The testimony of a triangular trio
Something more needs to be said about the remarkable event that is observed to occur in the denary realisation of the triangular number series: 6, 36 (or 6.6), 66 and 666 are all present. We ask whether these visual 'stepping stones' - involving the first perfect number as the repeated digit - are unique to the denary system. If it can be shown to be so then this, in itself, is powerful testimony for the absolute significance of ten.
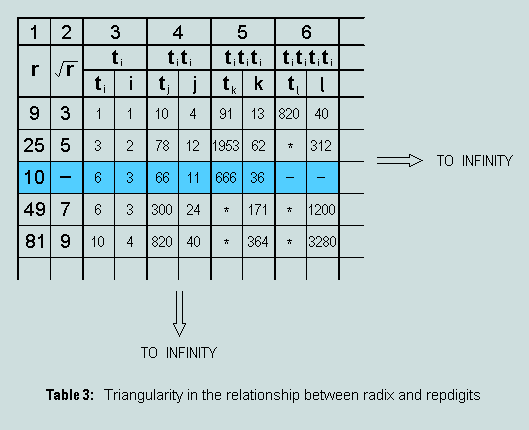
Clearly, 10 as radix is not at home in this company; it is the only even number and the associated sequence {6, 66, 666} is finite. Within the limits of Visual Basic 'long integer' arithmetic no other examples of the phenomenon have been found.
9 - The Pythagorean triples
The sequence of natural numbers reveals an infinitude of triples of the form {a, b, c} such that a^2 = b^2 + c^2. Geometrically, the implication is that the number of right-angled triangles whose sides are whole numbers is limitless. Focusing on these triangles we find, (a) the area is an integral multiple of 6 and, (b) the product of the sides is a multiple of 60 - ie ten times six. These features are completely independent of radix; they are absolutes.
There is an infinite series of numbers which we may conveniently refer to as the G-series - all members of which - when represented as denary objects - have a reduced digit sum (RDS - see #5 above) of 1 (or, alternatively, when divided by 9 leave a remainder of 1). The nth term in this series is given by (9n - 8). Here are its opening terms:
[1], [10], 19, [28], 37, 46, [55], 64, 73, 82, [91], 100, 109, 118, 127, [136], 145, ...
We observe, (a) the presence of 10 and 100 (indeed, it can be shown that all integral powers of 10 reside in the series), (b) the second perfect number, 28, is there (it can be shown that all perfect numbers - except the first, 6, are included), (c) all triangles, like 10, capable of generating symmetrical hexagons and hexagrams by self-intersection/-union are included (these are enclosed in square brackets) and, (d) two-thirds of all hexagons and hexagrams (generated, as described) are present. As has already been observed, the penulimate step in the RDS procedure yields 10, the system radix.
11 - The numerics of Genesis 1:1 and The Creator's Name
The seven Hebrew words of the Bible's first verse - read fairly as natural numbers - total 2701, or 37 x 73 - the 73rd triangular number. In the following table, the calculation '2701 = 37 x 73' is expressed over the range of radices 2 - 36; the triplet under the heading 'RDS' represents the corresponding reduced digit sum of Genesis 1:1 and of each of its factors, respectively.We immediately observe, (a) digit reflection in the prime factors occurs only when the radix is 10 and, (b) the factors together with their product are G-numbers; in other words, the digit totals equal the radix of the system in which they are represented, viz denary, and the RDS of each is 1; over the range 5 to 36 the only even radix to support this feature is 10.
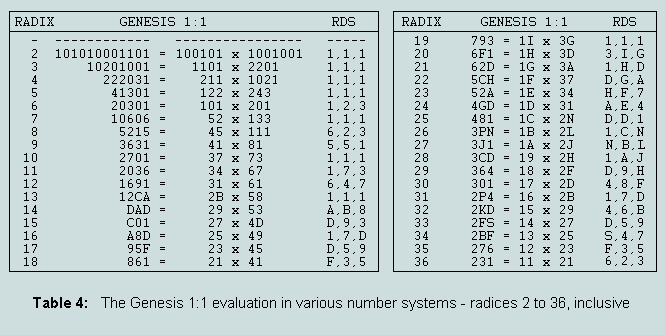
Observe also that only in the case of denary representation do we find the factors 37 and 73 revealed when the verse total is added to its digit reverse, thus: 2701 + 1072 = 3773.
Another prominent feature of Genesis 1:1 is 703, or 19 x 37 - the 37th triangular number - derived as the sum of words 6 and 7, translated "...and the earth." As with the complete verse we find each of the digit sums to be10 - radix of the system in which these numbers are represented. Again, on other pages at this site it has been shown that the Creator's Name ('Jesus Christ'), as rendered in both Septuagint and NT Greek - nominative case - is 2368, or 64 x 37 - the three groups of digits each summing to 10. Remarkably, these corresponding features may be displayed pictorially using the triangular representation of ten, as follows:
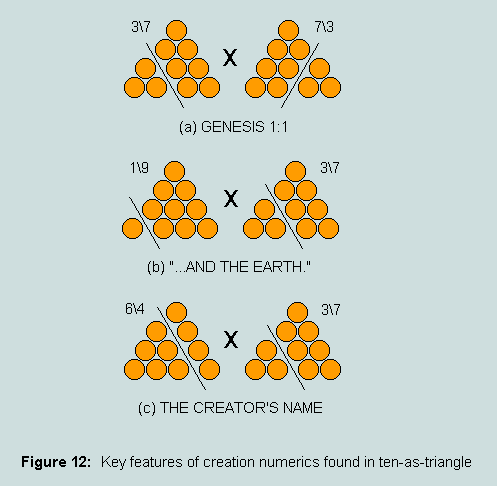
At (a), we find all the 'ingredients' of thirty-seven and seventy-three, respectively - the first being 3 x (3 + 7) + 7 and the second, 7 x (7 + 3) + 3. (b) and (c) follow in similar fashion - generating 703 and 2368, respectively.
12 - A solid partnership
We conclude this survey by making a simple observation concerning 3 and 6 (already related as triangular numbers - see #2.4 above). The reciprocals of these, as normally expressed, are 0.33333... and 0.166666..., respectively. In other words they replicate themselves as infinite sequences - the first, perfectly, and the second, only after that initial '1'. Clearly, these phenomena are mediated by ten. Change the radix, and they disappear.
13 - Conclusions
As early as the sixth century BC the importance of ten was recognised - particularly by the Pythagoreans who revered (even worshiped!) the tetraktys (its triangular representation). Since that time, much additional evidence has accumulated to substantiate the claim that it is indeed a significant numerical absolute - admirably fitted (and divinely intended) for use as a collective unit in the affairs of men. It should not escape the reader's attention that the remarkable number 666 has played a major role in establishing this fact. This number appears, of course, as a 'surface feature' in the biblical text (Rev.13:18) where it is found associated with, (a) the reading of a string of letters as a number and, (b) the offer of wisdom to those who strive to understand it (ie 666). In view of its application here in support of ten, it would appear that some grain of the promised wisdom has already been been received.
Vernon Jenkins MSc
2003-03-26
For further information regarding the remarkable properties of 666:
http://homepage.virgin.net/vernon.jenkins/sixes.htm
http://www.BibleWheel.com/GR/GR_666.asp
>>> Back to Main Index - page 1 >>>