PART 2 - Langton's Legacy

1. Introduction - It is widely acknowledged that circa 1200 AD the Englishman Stephen Langton - later to become Archbishop of Canterbury (1207-1228) - set about dividing the 66 books of the Bible into 1189 chapters to facilitate citation. The Wycliffe Bible of 1382 was the first to use Langton's scheme; since then it has become the standard for all but a few Bible translations. [Further information available here].

2. A secular focus of attention - Reference has already been made to a rare phenomenon of bifigurate numerical geometry, viz the matter of 'square = triangle'. It may be remembered that the specific example quoted earlier was 36 - 6th square and 8th triangle. The following table lists the first six instances of the phenomenon - these occurring within the range 2 to 2 billion. Attention is directed in particular to the 4th instance (shown highlighted).

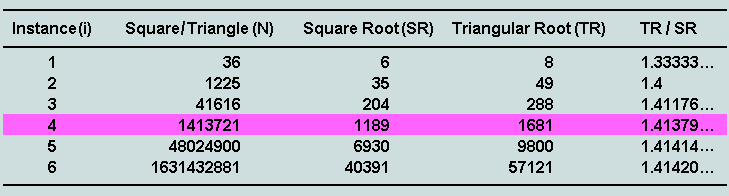
Table L1 - Equality of squares and triangles over the range 2 - 2 billion

Observe that 1413721 uniform circular counters may be arranged on a flat surface to form a square (or rhombus) comprising 1189 rows of 1189; or, alternatively, an equilateral triangle standing on a base of 1681. The following diagram is intended to help clarify the matter.

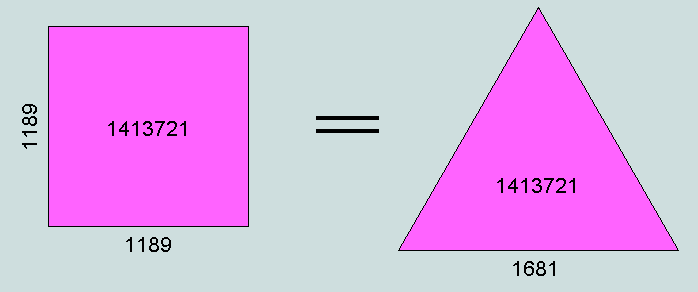
Fig. L1 - The square of 1189 = 1681st triangle

Now observe the following:

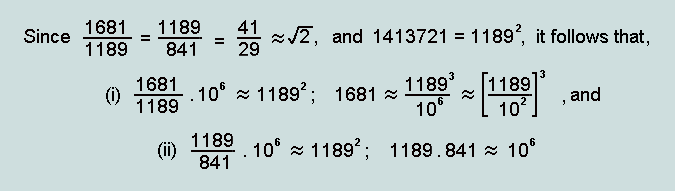
3. Enter an abundant modern artefact - ISO 216: 1975 established a number of international standards for cut paper sizes - most notably, the so-called A-series which - the USA and Canada excepted - has been adopted worldwide. Here's how the A-series is defined:

The rectangle having an area of 1 square metre and sides in the ratio square root of 2 to 1 measures 1189.207115...mm by 840.896415...mm. Since the standard requires lengths to be given to the nearest mm, these are rounded to become 1189mm x 841mm; this means that the actual area is 0.999949 m^2 - an error of 0.005%.

The following graphic is provided as an aid to the understanding of these details.

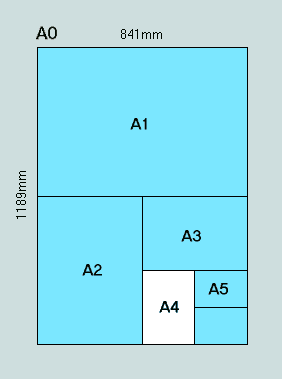
Fig. L2 - The A0 sheet and its subdivision

Observe that outcome (ii) above tallies precisely with the dimensions of the A0 sheet - base of the A-series of cut paper sizes.

Note that the particular significance of A4 (297mm x 210mm) in respect of its relationship to the numerics of Genesis 1:1 is treated in detail here and here.

4. Langton's chapters

The outcome of Langton's magnum opus was a biblical text divided into 1189 chapters - 929 for the Old Testament and 260 for the New.

Observe that 1189 is the 3rd element of the mid-point sequence whose root is 298, thus: 298 -> 595 -> 1189 -> 2377 ...

Fig. L3 - 595-as-triangle

At (a), we have an unembroidered picture of 595 which, at (b), it is revealed as a G-triangle, i.e. one comprising a number of outline triangles centred around a single counter. Recollect that such triangles are capable of generating hexagon/hexagram pairs by self-intersection/union. But there is more: 595 is the triangle obtained as an assemblage of 9 triangles of 66 centred around a single counter (see Fig. 7 of 'Balancing the Books'). Here is the essential diagram (centroid counter rendered purple):

Fig. L4 - 595 as an assemblage of 9 x 66-as-triangle

And, of course, as we have already seen, the number of books in the Bible happens to be 66!

Fig. L4 - 1189-as-hourglass

Significantly, Psalm 117 (one of the so-called Hallel psalms) is not only the Bible's central chapter, but it is also the shortest, and takes the form of a universal and powerful exhortation, thus:

"O Praise the Lord, all ye nations: praise him, all ye people. For his merciful kindness is great toward us: and the truth of the Lord endureth for ever. Praise ye the Lord." (AV)

How remarkable that these particular words should be brought to our attention at this time - and in this manner! Backed up by the truth of simple mathematics, they surely become irresistible.

5. One more thing! - The following discovery - which serves to consolidate the uniqueness of Psalm 117 - was recently brought to the author's attention by the researcher Stephen Coneglan. To understand this it is necessary that we briefly consider the numerical structure of the Psalm as it is found in the original Hebrew.

Fig. L5 - The numerical interpretation of Psalm 117

The complete Psalm is depicted here. Observe that it comprises 62 letters: 29 in the first verse and 33 in the second; ignoring the hyphens, it is clear that the first verse has 8 words and the second, 9. The values of the letters - read as numerals - appear above the text, and their respective sums - represented in blue - below; the verse totals are therefore 1080 and 1214, and the total for the complete Psalm, 2294. Like 2701 - the value represented by a similar alternative reading of the Hebrew of Genesis 1:1 - this is a multiple of the uniquely symmetrical number, 37 - thus, 2294 = 62 x 37.

With these basic numerical statistics to hand it now becomes possible to appreciate Stephen's insight. Here is how he describes it:

Psalm 117 is the shortest of the Bible's 1189 chapters, having just the two verses. Being the 595th means it is also the central chapter. Apart from the geometrical implications of its positioning as a point of balance within the structure of the Bible, the psalm itself contains its own remarkable numerical balance in regards to both word and letter count.

Word count:

Letter count:

Those are the details of the numerical balance found within the word and letter structure of Psalm 117. It is hard to see them as being anything other than purposefully weighted and meted out, especially in light of the dual signification of Psalm 117 as shortest AND central chapter of Scripture.

To obtain some idea of the comparative rarity of these combined features a computer simulation was carried out by the author on the complete Hebrew text of the Torah. The total of words (hyphens ignored) is 79,976; this means that the text offers a total of 79,960 sequences - each of 17 words - for analysis. Here is a summary of the findings:

Of the 79,960 sets of 17 words

75 satisfied the 1st pair of conditions (those involving the words)

3725 satisfied the 2nd pair of conditions (those involving the letters)

9 satisfied both pairs of conditions

In other words, the numerical structure of Psalm 117 delivers an attention-seeking 1 in 8884 longshot in respect of this feature - and that in addition to divisibility by 37, shortest chapter and central position!

6. Further comments - Laying aside the developments which culminated in the publication of ISO 216:1975, we are surely justified in questioning the remarkable coincidences that attend Langton's division of the biblical text into precisely1189 chapters. Did he begin his work with this number already in mind? Unlikely, I suggest; as a prolific writer of scriptural commentaries his prime purpose would have been to facilitate communication with his readers. Rather, like those many individuals involved in formulating the Christian Canon of 66 books, I suggest that Stephen Langton was fulfilling - albeit unwittingly - a further divine requirement that the number of chapters be 1189. The reason? IMO, simply to help this current generation accept the reality of a watermarked Bible - and begin, seriously, to consider the profound implications of such divine action.

Vernon Jenkins MSc

www.otherbiblecode.com

2005-07-14

 

The original page "Balancing the Books - The Eye-Opener" may be found here.

Suggestions for further reading:

"Exceptional Measures"

"The Postscript"