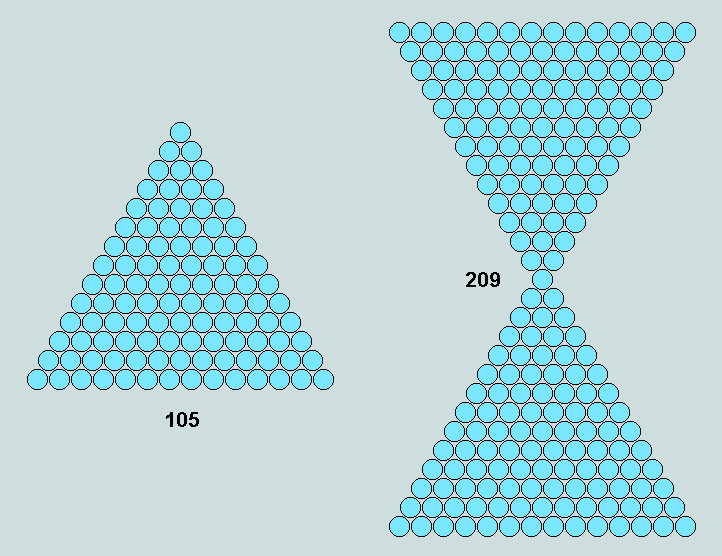
An introduction to midpoint sequences and the hour-glass

At the centre of every odd number (N, say) lies another (M, say) - where M = (N+1)/2. Clearly, M may be odd or even. If odd, then a sequence of two or more such centres may be obtained by repeating this procedure on successive outcomes until an even number appears to terminate the sequence.

As an illustration, consider the case in which N = 833. This leads to the following sequence of 6 midpoints:

833 ----> 417 ----> 209 ----> 105 ----> 53 ----> 27 ----> 14

From an analytical point of view this sequence is better viewed in reverse, thus:

14 ----> 27 ----> 53 ----> 105 ----> 209 ----> 417 ----> 833 ----> 1665 ----> 3329 ----> ... without limit

From this we learn that in choosing 833 as our starting value we were actually breaking into an infinite sequence in which each term after the first is double the previous term, less 1. Clearly, what we may conveniently term the root of such a sequence is some even number (E, say) - the sequence itself may then be referred to as S(E), so that in the foregoing example we view the opening terms of S(14).

We may represent the general sequence as

S(E) = M(0), M(1), M(2), ..., M(R) ..., M(R+1), ... to infinity, where the root of the sequence, M(0) = E.

Should any of the terms happen to be a triangular number then the next following term may be represented geometically as an hour-glass. As an example, consider M(3) of the sequence S(14) above. Its value is 105 - 14th triangular number. This is depicted in the following diagram along with M(4), or 209, in hour-glass form.

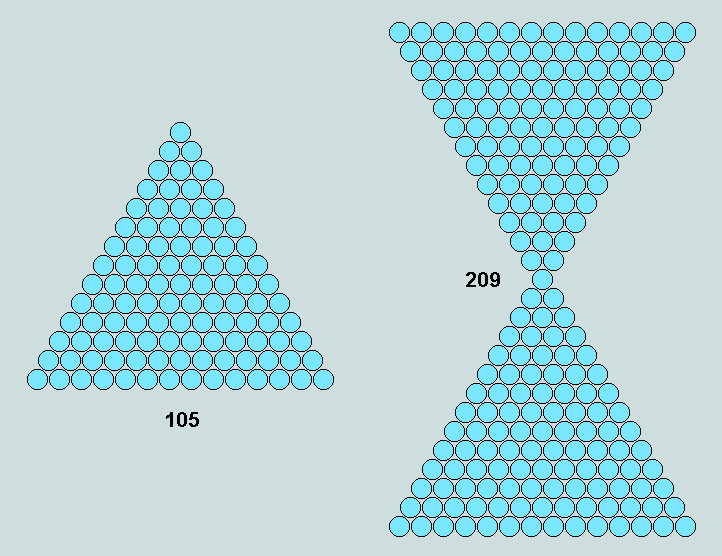
Vernon Jenkins MSc

2005-4-23