Appendix 2 - Some observations on squares and square roots

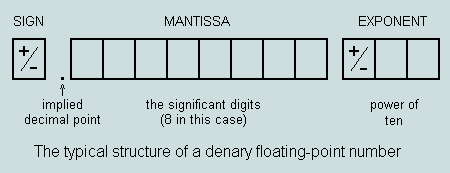
For the purposes of this analysis a real number (ie one which normally incorporates a fractional component) is expressed in floating-point notation as the ordered set: sign - mantissa - exponent. Observe that in standard computer practice strings of binary digits would occupy each of these three fields. Here we shall follow the simpler plan depicted below.

Now consider the two numbers A = 64. 00 and B = 640.0 - the second ten times larger than the first. Expressing each in terms of the foregoing format, we have:

Observe (a) that the mantissa fields are identical, and (b) that the movement of the decimal point from its 'home' position is respectively 2 and 3 places to the right - as indicated by the positive exponent fields.

The question now arises, What happens when we take the square root of each of these numbers? Here are the respective outcomes:

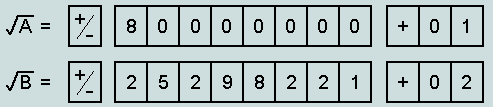
Observe, (a) that the mantissa fields are now completely different; and whereas the first is precise, the second - being a truncated version of an infinite string of digits - slightly undervalues the true result. (These matters are made clear by squaring each of these results to find that whilst A has been retrieved precisely, B has become 639.99998), and (b) that the ratio : = = 3.1622776.

Now let us apply these principles to the derivation of the fine structure constant (). This, defined as the square of the coupling constant, has the value 0.007297352533 with an uncertainty of 27 centred on the last two digits. Let us therefore focus on the first 8 significant digits of (which are accepted as fixed).

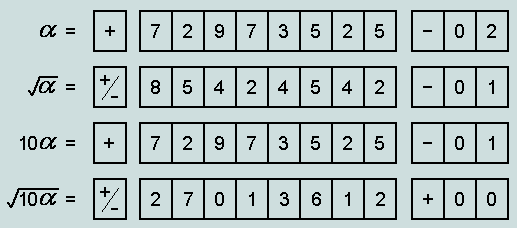
Observe that the second entry features the accepted value of the 'coupling constant', viz -0.085424542, of which is the square. Using precisely the same mantissa field, but incrementing the exponent field by 1, we have the representation of 10 depicted in the third entry. The square root of this is given in the final line where we observe the first 4 significant digits of the mantissa to be '2701'. Reading this as a number in its own right, we recognise the characteristic value (CV) of Genesis 1:1, 73rd triangular number! It follows, therefore, that squaring this number (, say) must yield a scaled approximation of . And so it proves:

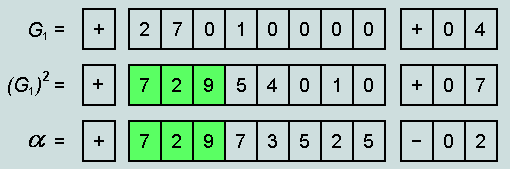
Clearly there is correspondence in the first 3 significant figures. The difference between the two mantissa fields is 19515 which represents an error of -0.027%, or 1 part in 3739, in the estimation of a scaled version of . But let us now recall that = 27013612, ie the concatenation of 2701 with 3612; and observing that Genesis 1:1 is linked physically with Genesis 1:2 (, say) and semantically with John 1:1(, say) we are interested to discover that = 3546 and = 3627 - these straddling 3612 and within a percentage point or so of it.

Here are the implications of concatenating the characteristic values (CVs) of the Bible's first two verses (, say):

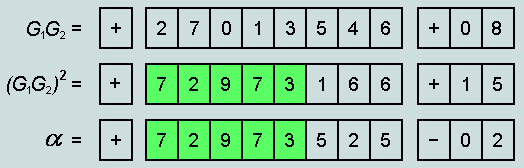
Observe there is now correspondence in the first 5 significant figures. The difference between the two mantissa fields is -359; this represents an error of only -0.0005%, or 1 part in 203,269, in the estimation of .

Finally, here are the implications of concatenating the CVs of the subject-related verses, Genesis 1:1 and John 1:1 (, say):

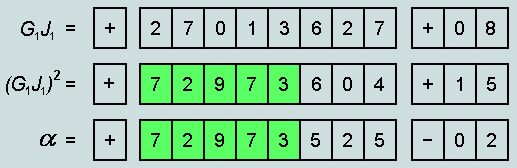
Again, we observe correspondence in the first 5 significant figures, with now a mere +79 difference in the mantissa fields. In this estimate of the error is therefore +0.00001%, or slightly in excess of 1 part per million.

In each of these later procedures observe that Genesis 1:1 assumes the dominant role by providing the 4 most significant figures - Genesis 1:2 or John 1:1 supplying the 'fine-tuning'. This, of course, is most appropriate, (a) because it precedes the others in the biblical text, and (b) because of its pre-eminent numero-geometrical structure.

Vernon Jenkins MSc

2003-11-26