Appendix 3 - An introduction to the Ulam spiral

The Ulam spiral is a graphically concise way of representing long sequences of the natural numbers, of highlighting properties that may be held in common, and of detecting patterns of behavior that would otherwise be largely unknown. Here's how it works:

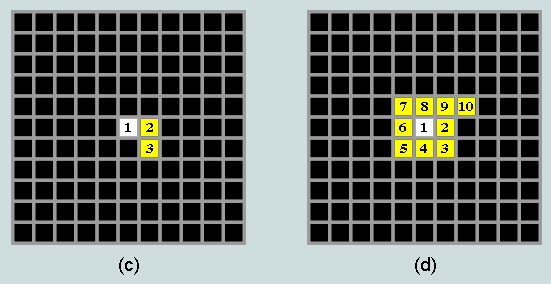
(a) Assign the value '1' to the cell at or near the centre of a square grid. (b) Mark the adjacent cell on the right '2'.

Proceeding in clockwise 'swiss-roll' fashion, continue the sequence in successive cells, as at (c) and (d) as far as may be required.

As a practical application of this method of portrayal consider the representation of the prime numbers over the ranges 2 - 121 and 2 - 51984, respectively. At (e) the 11x11 grid of cells centred on the origin (marked 1) is seen to accomodate the first 30 primes (ie 2,3,5,7,...107,109,113); at (f), where each cell is reduced to a single pixel, the first 5318 primes are depicted.

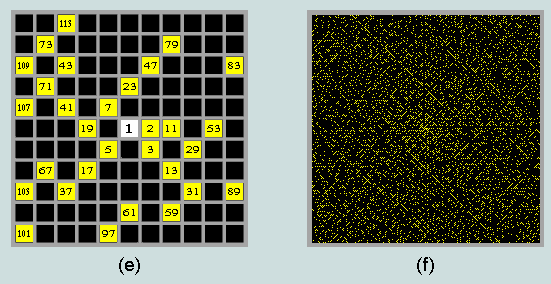
Clearly, the horizontal, vertical and diagonal lines that are visible in (f) reveal a degree of structure in this important subset of the positive integers that would otherwise have escaped attention!

The triangular numbers also reveal interesting patterns when plotted on the Ulam spiral.

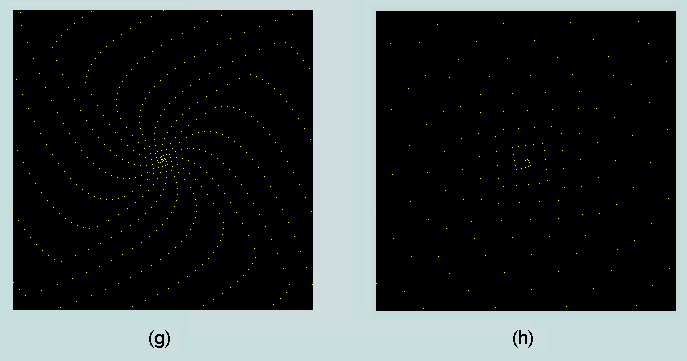
At (g), we have the first 423 triangles of the general series depicted on a 300x300 pixel grid; at (h), the 140 generator triangles contained within the same range.

Vernon Jenkins MSc

2003-08-04