Some Geometrical Restructuring

[An explanation of the fair reading of Hebrew and Greek words as numbers is provided here].

Observe that the sum of words 1 to 5 is 1998 (or 3 x 666, or 2 x 999, or 54 x 37); that of 6 and 7, 703 (or 19 x 37); and that of the whole verse, 2701 (or, 73 x 37). Here is a triangular realisation of these data:

The purple annulus (containing 1998 counters) together with the green triangle (containing 703 counters) form the triangle representing the verse total, 2701. Observe that the triangles share a common centroid (rendered white). When the inner triangle is rotated through 180 degrees the annulus is trisected, thus:

Observe, (a) the precise coordination between the triangular forms of 703 and 2701 and, (b) the emergence of three more triangles - each formed of 666 counters.

In an alternative geometrical representation, Genesis 1:1 appears as a trapezium of height 37 units, centred within which is 703-as-triangle, thus:

In this layout the flanking parallelograms each comprise 999 counters (913 + 86, on the one hand, and 203 + 401 + 395, on the other).

Further interest is created when the 7 words of Genesis 1:1 are divided in order, thus: 913 + 203 = 1116 = A, say; 86 + 401 + 395 = 882 = B, say; and 407 + 296 = 703 = C, say.

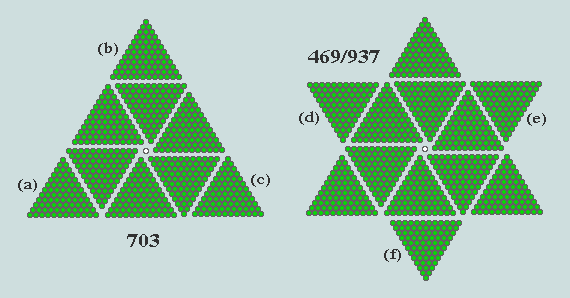
Observe that while [A + B] = 1998 (which integrates beautifully with C, as we have seen), [A - B] = 234. But how, if at all, does this integrate with C? Remarkably, we find (C + 234) = 937 = the hexagram formed from the self-union of C-as-triangle; and (C - 234) = 469 = the hexagon formed from the self-intersection of C-as-triangle. These wonders are depicted below.

On the left we see a representation of C, and on the right, its union with an inverted copy of itself. The result is a hexagram of 937 units (represented by the whole figure) and a hexagon of 469 units (represented by the overlap).

The explanation for this remarkable outcome is straightforward: recall that a 1-centred triangle (i.e. one capable of generating a hexagon/hexagram pair in the manner shown above) is itself constructed from 9 elemental triangles (drawn from the general series) disposed symmetrically about a single central counter, thus:

On the right, we observe the derivatives, hexagon and hexagram, comprise 6 and 12, respectively, of the same elemental triangle.

In the case of 703, the elementals are 78 (= 12th triangular number) apiece. The difference, (A - B) - which we found to be 234 - is seen to be 3 x 78; that is, three times the elemental of 703. Hence, removing the 3 elementals, (a), (b) and (c), from the triangle leaves the hexagon; whilst adding the 3, (d), (e) and (f), yields the hexagram.

Vernon Jenkins MSc

2007-02-19

Acknowledgement: The author is grateful to Richard McGough who brought this feature to his attention.