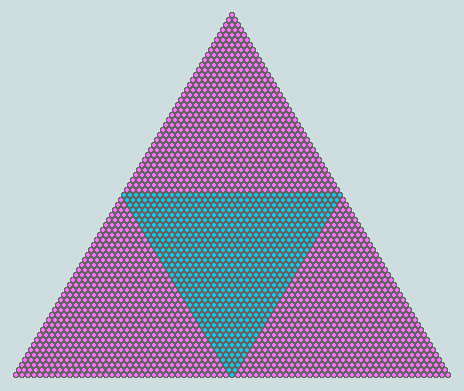
We have already observed that the outline of the Genesis 1:1 triangle comprises 216 counters - 216 being the cube of 6. Thus an important link with the Platonic Solids has already been forged. Observe that three of the remaining four regular polyhedra have triangular faces, viz tetrahedron, octahedron and icosahedron. Of these, only the tetrahedron and octahedron lend themselves to a numero-geometrical representation - as depicted in the pictures which follow.

It follows that the coordinated triangles of Genesis 1:1 may be taken to represent the face of a numerical tetrahedron (specifically, the 73rd) inscribed with the face of an octahedron (specifically, the 37th) - this solid surmounted by 4 tetrahedra of order 36 (providing the visible faces of the 3 remaining triangles). Certain important implications follow which are discussed below.

Here again is the diagram depicting the 2701 / 703 relationship (involving the verse total, and sum of words 6 and 7, respectively):

In order to better comprehend the subsequent argument some further pictures are appropriate:

At (a), we see a cardboard model of a composite tetrahedron which is progressively deconstructed at (b), (c) and (d) to reveal the 4 smaller tetrahedra surmounting the octahedron.

The following diagrams show how equivalent numerical models may be realised as stacks of uniform spheres:

At (a), we have a model of the 7th numerical tetrahedron - sum of the first 7 triangular numbers, i.e. 1+3+6+10+15+21+28, or 84. The stack depicted at (b) incorporates an octahedral core (c) of 44 - this surmounted by 4 numerical tetrahedra of dimension 3. Each of the 4 faces of this composite is an analogue of the earlier Genesis 1:1 picture.

The formulae that enable us to determine the number of counters involved in these figures are as follows - n being the order number (i.e. the number of spheres forming an edge):

First, the tetrahedron: Q(n) = n(n+1)(n+2) / 6; then, the octahedron: O(n) = n(2n^2+1) / 3

Check: in the foregoing models, Q(7) = 7.8.9/6 = 84; O(4) = 4(2.4^2+1)/3 = 44

We are interested in Q(73), Q(36) and O(37) - the solids involved when the Genesis triangle is understood to represent the face of a tetrahedron; these are 67525, 8436 and 33781, respectively. All three are significant: 67525 = 25x2701; 8436 = 12x703; and 33781 = 37x913 - this latter being the product of the principal factor of Genesis 1:1 (and uniquely symmetrical as a number per se) and the sum of its first 6 letter values (which form the Bible's first word), thus:

Persevering with the suggestion that 2701-as-triangle (73rd in the general series - and sum of the first 7 words) with an inverted 703-as-triangle (37th in the general series - and sum of words 6 and 7) inset is really the face of a tetrahedron having an octahedral core, then it is natural that we should consider 3003-as-triangle (77th in the general series - and sum of the first 8 words) also to be the face of a tetrahedron. Now observe that because the difference in the order numbers of these regular solids is 4, (i.e. 77-73) then the larger can be envisaged as perfectly encapsulating the smaller - in effect, protecting it in the same manner as the kernel of a nut is protected by its shell. Here are some further pictures which demonstrate this principle:

At (a), we see the triangular base of the 7th numerical tetrahedron, and at (b), a complete tetrahedron of dimension 3 centred on this base. The beginning of the process of encapsulating the smaller solid is shown at (c); and completed at (d). Clearly, this principle extends to all pairs of such tetrahedra provided that the order number of the larger is 4 more than the smaller.

It thus appears that 3003, the triangle that embraces 2701, was no haphazard choice! The first word of Genesis 1:2 (and the first of the remainder of the Scriptures) is therefore seen to provide both a plinth (as depicted in #11 above) for Genesis 1:1-as-triangle and a protective cover for the related tetrahedron. The implication must be that the Lord considers this first verse to be a most important and precious object.

Vernon Jenkins MSc

2004-12-30