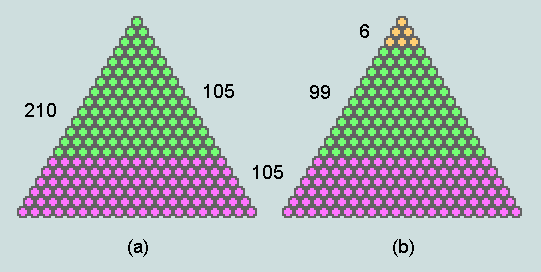
When a triangular number is doubled, the outcome is rarely itself triangular. Indeed, of the 1413 triangular numbers in the first million natural numbers, only 4 have this property, viz 3, 105, 3570 and 121278 (order numbers 2, 14, 84 and 492, respectively). Here, we are particularly concerned with the first two and their doubles, 6 and 210 (order numbers 3 and 20, respectively) - as depicted below.

The triangular formation of 210 counters (a) is shown evenly divided into a triangle and a trapezium - each comprising105 counters; at (b), the triangle of 105 is shown further divided into a trapezium of 99 and a triangle of 6. It is this latter situation that provides a fundamental backdrop to the following analysis of Genesis 1:1 and next following word. Here again are the relevant data:

This set of numbers gives rise to the following table of differences:

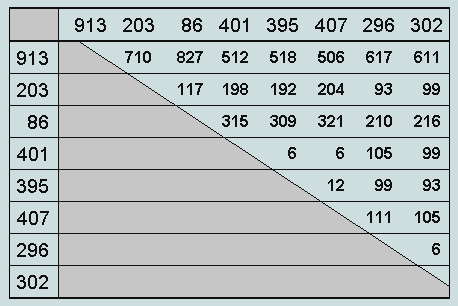
Each of the 28 entries in this table is derived from the values heading the row and column in which it occurs by subtracting the smaller from the larger. Thus, 710 = 913 - 203, and so on. [Clearly, to complete the table would be but pointless repetition].

Observe that included among these differences are the numbers which feature in the numero-geometrical singularity noted above, viz 99 and105, and their difference, 6 - as are their simple multiples, 12, 198, 210 and 315. Even those differences that remain - except the ones involving 913 - may each be readily expressed in terms of 99 and 105 only, thus,

93 = 2.99 - 105; 111 = 2.105 - 99; 117 = 3.105 - 2.99; 192 = 3.99 - 105; 204 = 99 + 105; 216 = 3.105 - 99; 309 = 2.105 + 99; 321 = 4.105 - 99. [Note the use of the period (.) here to signify 'multiplied by']

But we also observe that if 500 be subtracted from each of the differences involving 913 the residues fall in with the same scheme. Thus,

710 - 500 = 210 = 2.105; 827 - 500 = 327 = 5.105 - 2.99; 512 - 500 = 12 = 2.(105 - 99); 518 - 500 = 18 = 3.(105 - 99); 506 - 500 = 6 = 105 - 99; 617 - 500 = 117 = 3.105 - 2.99; 611 - 500 = 111 = 2.105 - 99.

[Of passing interest, 216 and 512 (the cubes of 6 and 8, respectively) are seen to be included in the table of differences.]

Clearly, these eight values - representing a natural alternative reading of the first eight Hebrew words of Genesis - which we might have expected to be numerically independent - are here shown to belong together - mediated by the parameters 500, 105 and 99. But, of course, these latter have been derived from the analysis of differences. Can there be a way of expressing the eight biblical values themselves in terms of these same parameters? The following table of parameter differences points the way:

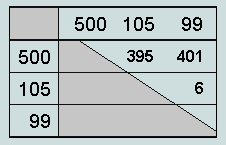
The difference between the first two parameters is seen to be 395 - value of the 5th word; and that between first and third, 401 - value of the 4th word. We may thus anchor the floating set of differences to the extra-biblical absolute 500, and proceed to evaluate all 8 words in terms of the 3 parameters. Thus, for example, 296 = 395 - 99 = 500 - 105 - 99; 86 = 296 - 210 = 500 - 105 - 99 - 2.105 = 500 - 3.105 - 99; and so on.

The whole remarkable matter may now be formalised as follows:

If the set of 8 numbers under discussion be represented by G(i), i = 1 through 8, then we may write

G(i) = 500.A(i) + 105.B(i) + 99.C(i)

in which the variables A, B and C are represented by small integers, thus: