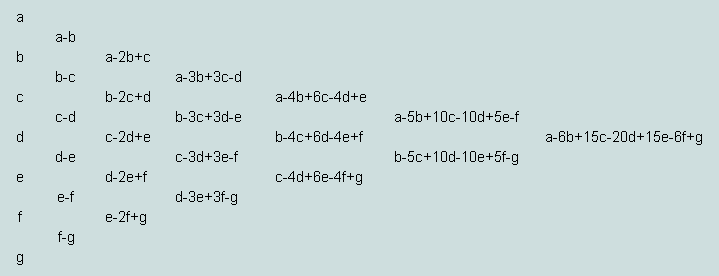
Appendix 2 - An aid to progressive differencing
In general, a progressive differencing operation involving the ordered set of 7 numbers {a b c d e f g} will assume the form shown below.
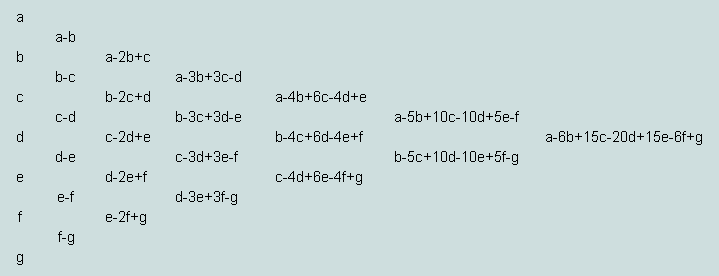
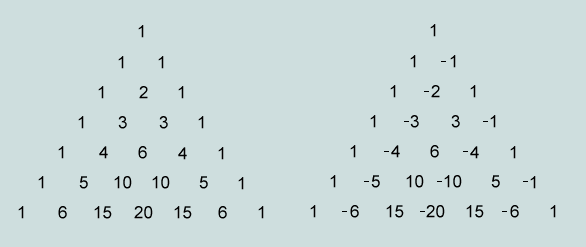
The coefficients of the entries in successive columns (reading left to right) are defined by the corresponding rows of a modified Pascal Triangle. In the following diagram, the original triangle (left) is shown again (right) with alternating signs across each row. It is the latter that defines the coefficients in the foregoing table of differences.
Thus, for the Genesis 1:1 set, we have in column 7
It may be remembered that the 7 Hebrew words of Genesis 1:1 comprise a total of 28 letters, and that 28 is 7th triangular number. There is therefore a geometrical correspondence between the original Pascal triangle depicted above and the letters of the Bible's first verse. Interestingly, the sum of the CVs of the latter, viz 2701, is a cyclic permutation of 0127, or 127 - the sum of the 28 elements of this triangle!
Vernon Jenkins MSc
2001-11-14