

1. Introduction
The so-called Golden Section refers to the division of a line such that the whole is to the greater part as that part is to the smaller part - a proportion which is considered to be particularly pleasing to the eye. Here is a depiction of the principle:
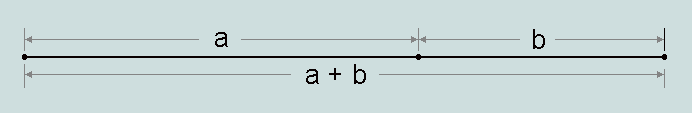
whence we have the related Golden Ratio, (a + b)/a = a/b, usually represented by the lower case Greek letter 'phi' (f).
This equation has as its unique positive solution the irrational number
(1 + ![]() ) / 2 =
1.6180339...
= f -------------- (i)
) / 2 =
1.6180339...
= f -------------- (i)
We read in the Wikipedia entry under this heading, "At least since the Renaissance, many artists and architects have proportioned their works to approximate the golden ratio - especially in the form of the Golden Rectangle, in which the ratio of the longer side to the shorter is the golden ratio...Mathematicians have studied the golden ratio because of its interesting properties."
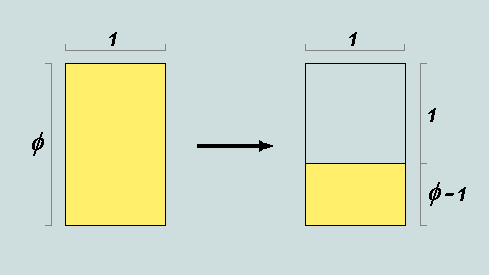
Observe that the rectangle generated by removing a square from the original figure is similar to it, i.e. its sides too are in the ratio 1:f, and we may therefore write f/1 = 1/f - 1. This leads to the two interesting outcomes:
f 2 = f + 1 --------------------------- (ii)
and
1/f = f - 1 -------------------------- (iii)
As has been demonstrated in earlier pages (details here), the three prominent universal constants p, e and a are implied by the Hebrew letters and words of Genesis 1:1 and its Greek cognate, John 1:1. Here, it is proposed to add f to this list. However, before that becomes possible, it is necessary that we establish clear links between f and certain trigonometric ratios - this, in turn, requiring an appeal to simple principles of geometry.
2. A geometric derivation of the golden ratio
The following diagrams depict a regular pentagon - i.e. one whose vertices lie on a circle and whose sides and diagonals form isosceles triangles. Observe that each number represented is an angle expressed in degree measure.
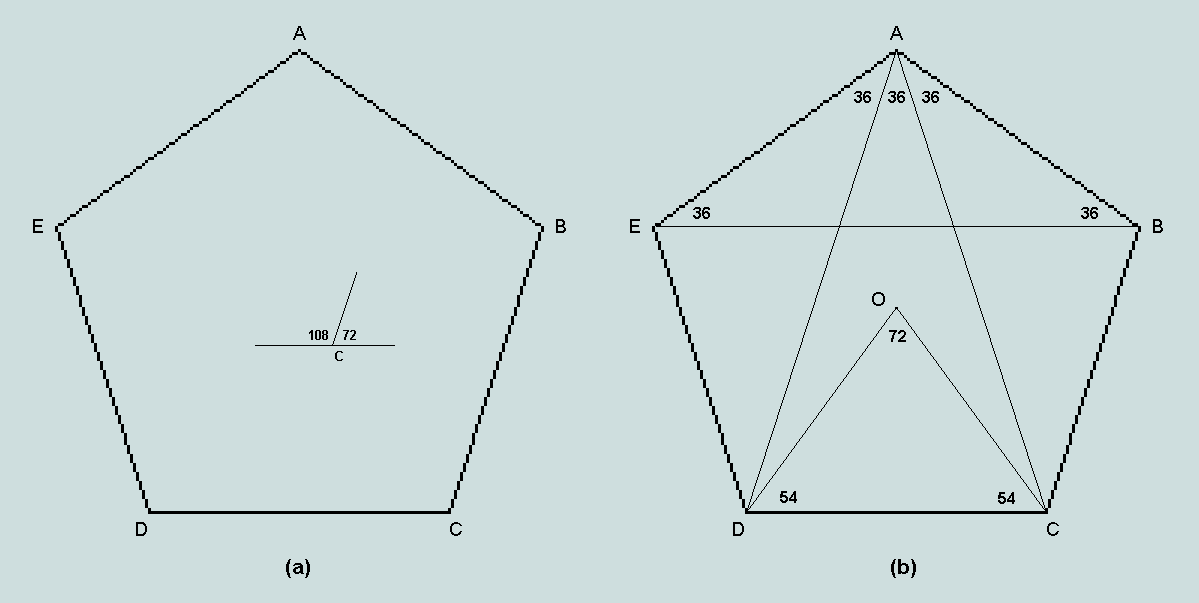
Since each exterior angle of the pentagon is 360/5, or 72, it follows that each interior angle is (180 - 72), or 108 [see inset at (a)]. At (b), O represents the centre of the circumscribed circle. Angle DAC is half the angle subtended at the centre - its value is therefore 36. The remaining angles are readily calculated - significantly, all are multiples of 18.
In the following developments, each of the coloured triangles is observed to be isosceles, and the green and blue triangles, similar. Thus, in particular,
EB/BA = BA/QB, whence
BA2 = EB.QB
= (EQ + QB).QB = (AE + QB).QB
= (BA + QB).QB
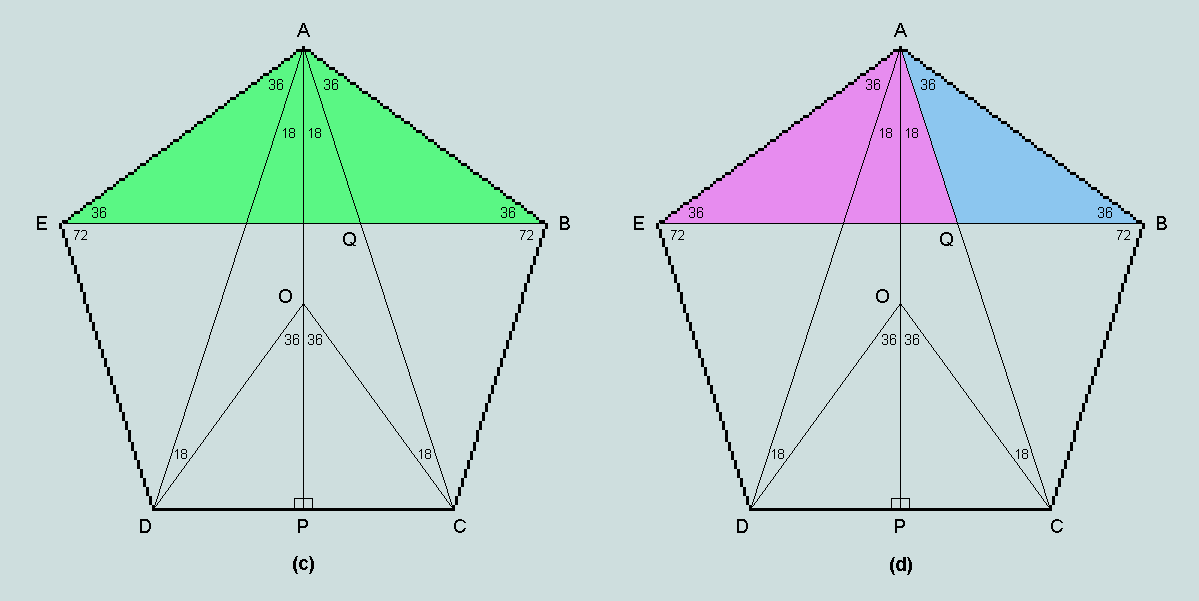
It therefore follows that
BA/QB = (BA + QB)/BA = 1 + QB/BA
and, setting the ratio BA/QB = x, we have
x = 1 + 1/x, or x2 = x + 1
whence,
x = (1 + ![]() ) / 2 = 1.618034...
= f, the GOLDEN RATIO ---------------- (iv)
) / 2 = 1.618034...
= f, the GOLDEN RATIO ---------------- (iv)
If the perpendicular, QR, now be dropped from Q onto AB (as in the diagram below), it follows that
BR/QB = f/2 = cos 36 = sin 54 -------------- (v)
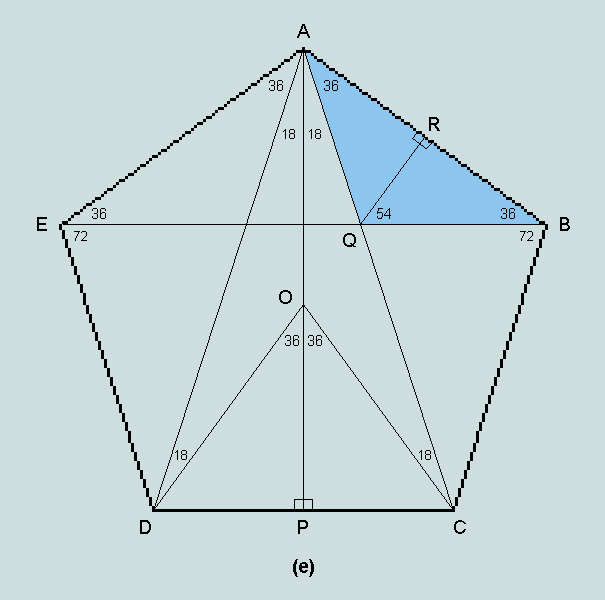
Because the trigonometric functions are periodic, these results extend to limitless sequences of angles - as the following diagrams make clear.
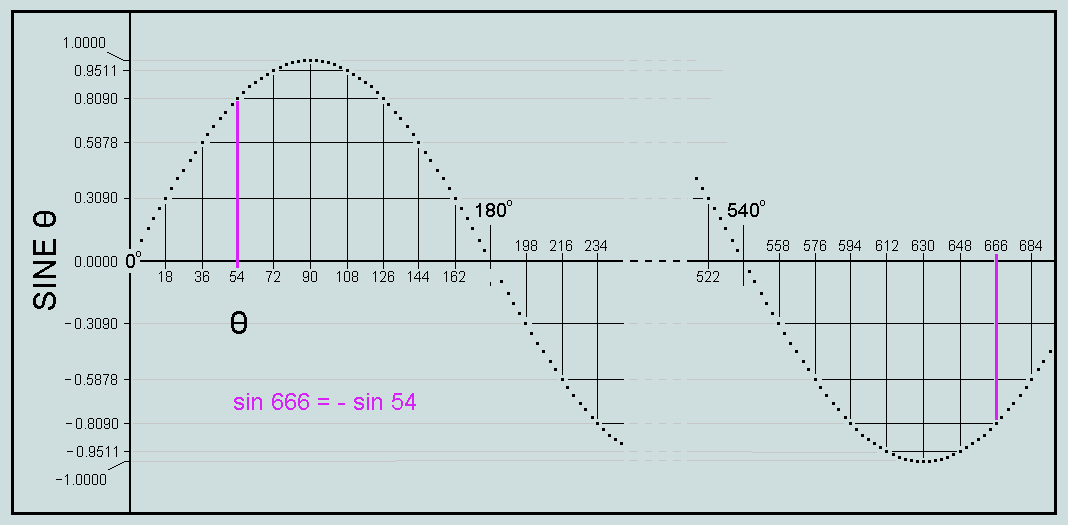
The outline of a typical sine curve is here represented by a series of points, q being a multiple of 3. Observe that the graduations on the axes refer to q a multiple of 18. Clearly, sin 54 = sin 126 = -sin 234...= -sin 594 = -sin 666 =...
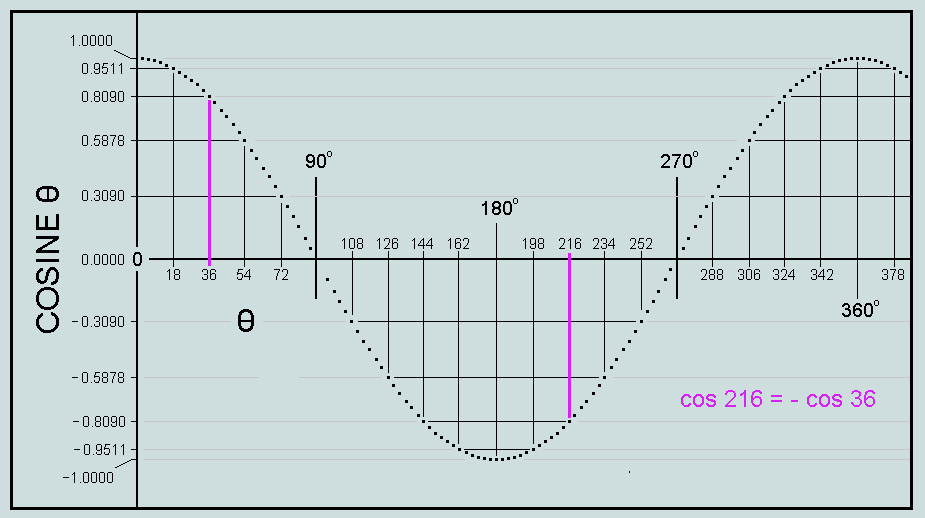
The corresponding cosine curve above similarly reveals cos 36 = -cos 144 = -cos 216 = cos 324 =...
Combining these observations therefore enables us to write
sin 666 + cos 216 = -f
whence,
f = - [sin (666) + cos (6.6.6)] ------------- (vi)
And what of 18, i.e. (6+6+6)? The following analysis shows that this angle too has a place in these proceedings. Here is the geometrical basis of the matter:
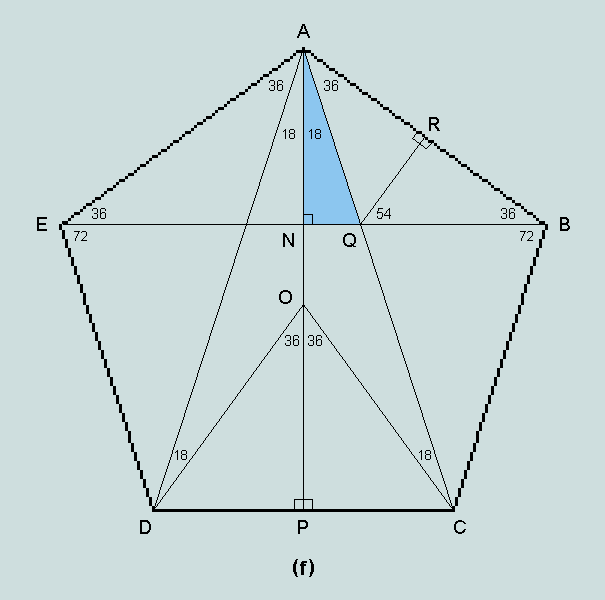
In triangle ANQ, sin 18 = NQ/QA = NQ/QB [triangle QBA isosceles] ----------------- (vii)
In triangle NBA, NB/BA = cos 36 = f/2 [from (v)], and
in triangle QBR, BR/QB = BA/(2.QB) = sin 54 = f/2 [from (v)]
Hence, NB = BA.f/2 and QB = BA/f
Clearly, therefore, NQ = NB - QB = BA.(f/2 - 1/f) = BA.(f2 - 2)/(2.f) and it follows from (vii) that
sin 18 = BA.(f2- 2)/2.f) / (BA/f)
= (f2 - 2)/2 = 1/(2.f) [since, from (ii) and (iii), f2 = f + 1, and f - 1 = 1/f]
Whence,
f = cosec(18)/2 = cosec (6+6+6)/2 ---------------- (viii)
[Observe that each of the foregoing results - linking the golden section (f) with trigonometrical functions of particular angles - may be readly confirmed if one has access to a scientific electronic calculator.]
3. The triples of sixes spanning the Judeo-Christian Scriptures
Attention is here drawn to just two significant instances of the relationships involving 666, 6.6.6 and 6+6+6.
(1) In the Book of Revelation, 666 is offered as a key to the gift of wisdom (Rev.13:18). A detailed consideration of this visually-arresting number reveals it to be not only triangular, but uniquely so; this because each of its numerical attributes is triangular - and, further, that the sum of these is 216, or 6.6.6. Here is a reminder of these details:
Observe that the radix-dependent attributes contribute 72, and the absolute attributes 144, to the combined total of 216 - and that 666, 72 and 144, are multiples of 18.
But note too the triangular representations of 6 and 10 that occur at each of the three vertices of the larger triangles - where the angle in degree measure is 60, or 6.10. Clearly, this is a feature common to all numerical triangles.
(2) As we have seen in earlier pages on this site, a geometrical view of the numerics of Genesis 1:1 - the Bible's first verse - reveals a symmetrical structure in which 666-as-triangle features, in triplicate, within a triangular outline of 216, or 6.6.6 - i.e. the 6th cube. These facts are recalled in the diagram below.
At (a), we have the composite structure of 2701 - the sum of the 7 Hebrew words of the Bible's first verse, fairly read as numbers. The first 5 of these total 1998, or 3.666 (represented by the purple triangles); the last 2 (translated "and the earth.") total 703 (represented by the green central triangle). At (b), the outline triangle (rendered white) comprises 216, or 6.6.6, counters.
4. Conclusion
The foregoing analysis makes it abundantly clear that this universal constant, f - whose history stretches far back into antiquity, and which, for a variety of reasons, has long fascinated man - has substantial links with the Judeo-Christian Scriptures. Against the backcloth of the p, e and a connections drawn from the same sources, it is hard to believe that such matters are fortuitous. Everything points to the fact that these texts are divinely authored, and contain far more information than has, formerly, been supposed.
Vernon Jenkins MSc
2008/09/01
2009/11/25 - corrected and extended