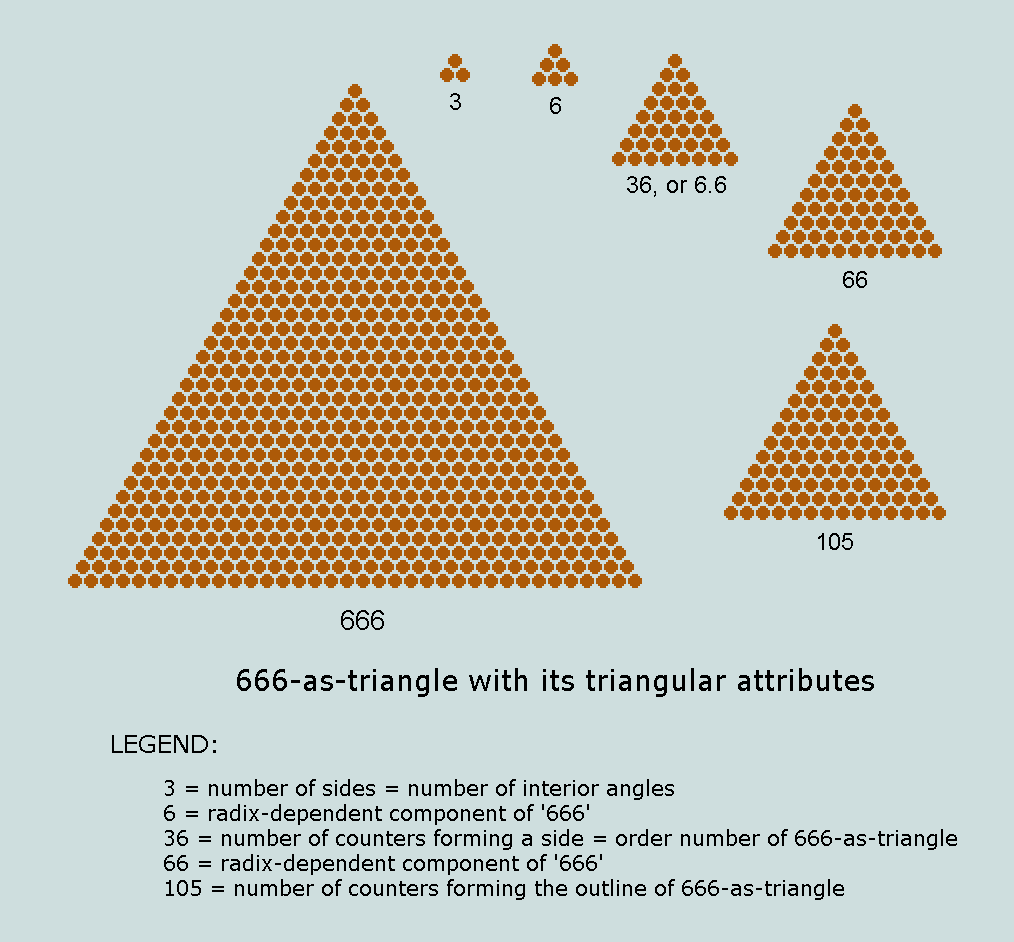
666: epitome of numerical triangularity

As depicted below, 666 pennies may be laid out in close formation on a flat surface to form the 36th numerical triangle. While, in general, triangular numbers are comparatively rare, 666 is unique - its uniqueness resting on the fact that all its numerical attributes are themselves triangles!

To further emphasise the remarkable singularity of this number, we observe,

(1) the sum of these attributes, 3+6+36+66+105 = 216, or 6x6x6!

(2) the highest prime factor of 666 is 37 - this being the only number whose counters may be arranged symmetrically on a flat surface in more than two distinct ways, thus:

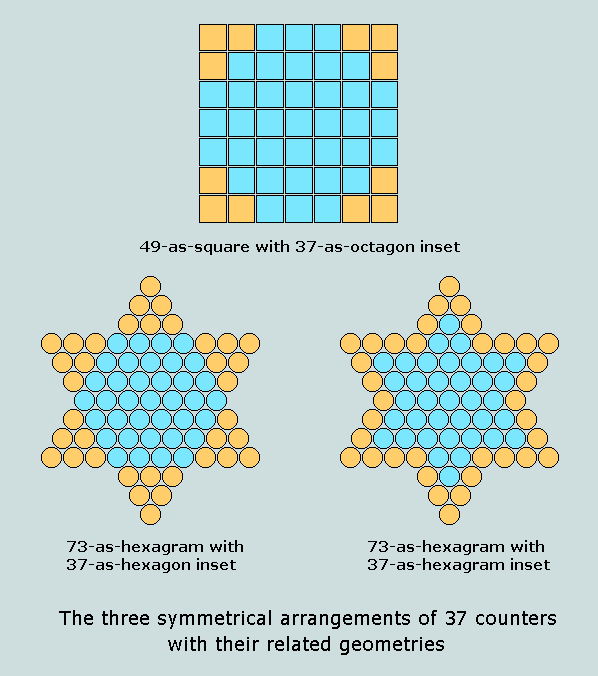
Observe here that, (a) for convenience, uniform square counters are used in the first of the structures depicted, (b) 73 (digit reverse of 37) is closely involved with both 37-as-hexagon and 37-as-hexagram and, (c) the latter are themselves amalgamations of numerical triangles

(3) that 666 may therefore be expressed as 18 x 37, or (6+6+6) x 37!

(4) the incidence of three sixes in the digits of the angular dimensions of all equilateral triangles, thus: