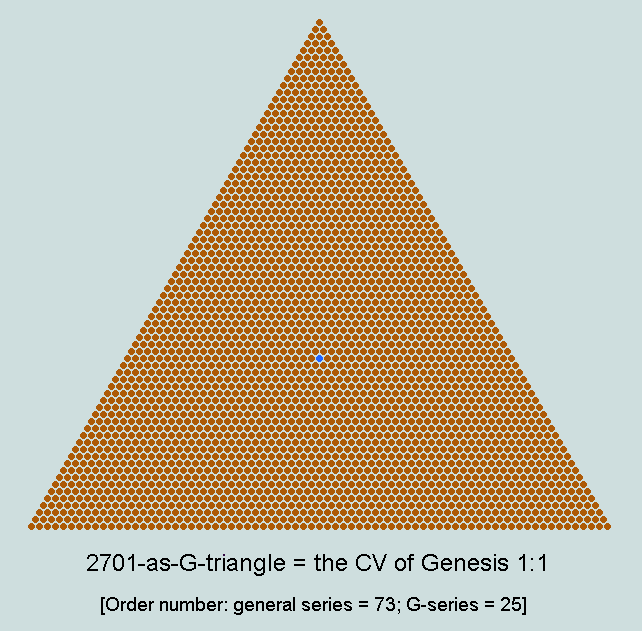
1801: rare example of a numerical hexagon

2701-as-triangle is capable of generating a hexagon/hexagram pair by self-intersection/self-union, as the following diagrams make clear:

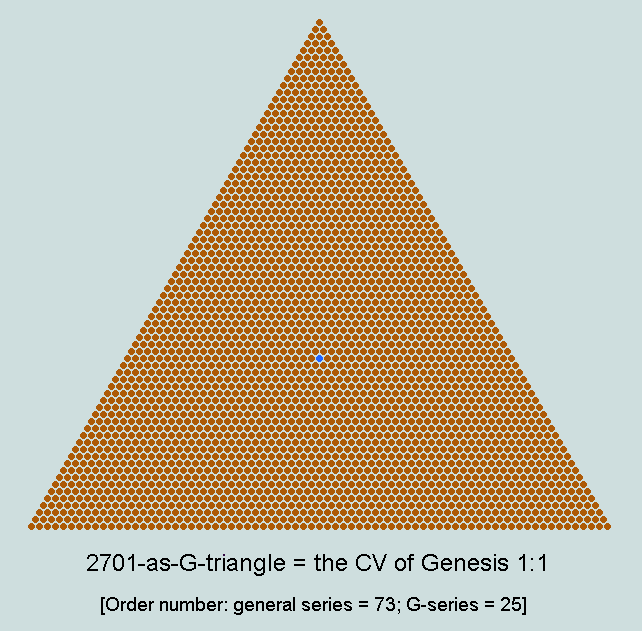
Observe that the centroid counter (here rendered blue) lies at the centre of the 49th row (as counted from top down), or 25th row (as counted from bottom up) - these ordinals the squares of 7 and 5, respectively.

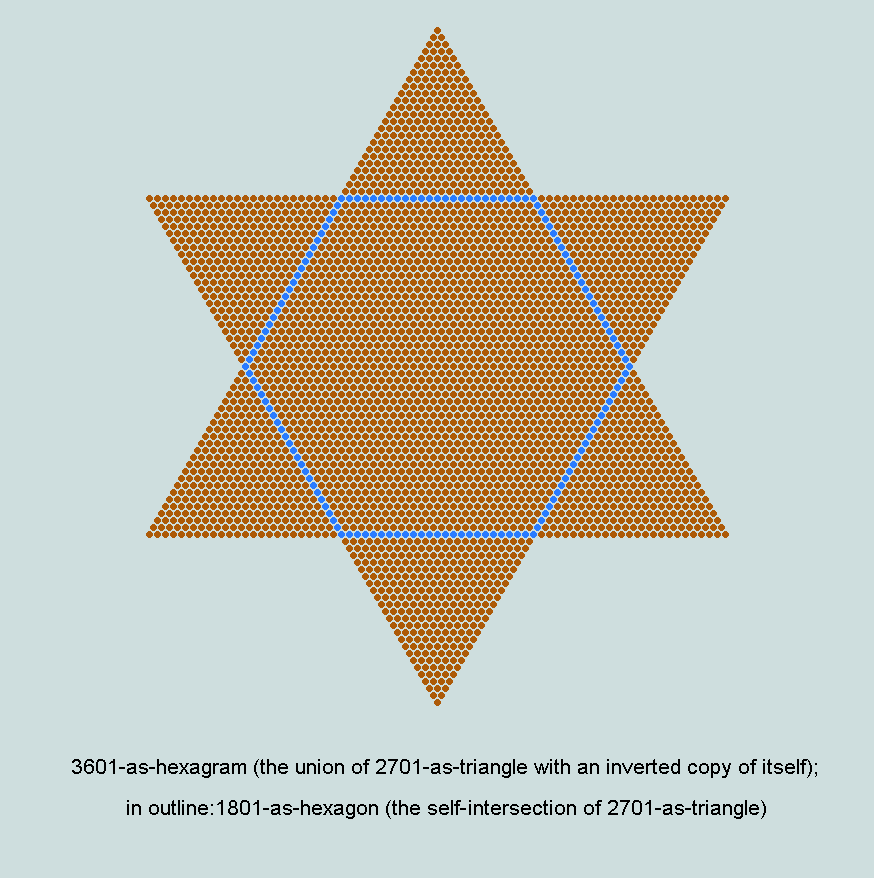
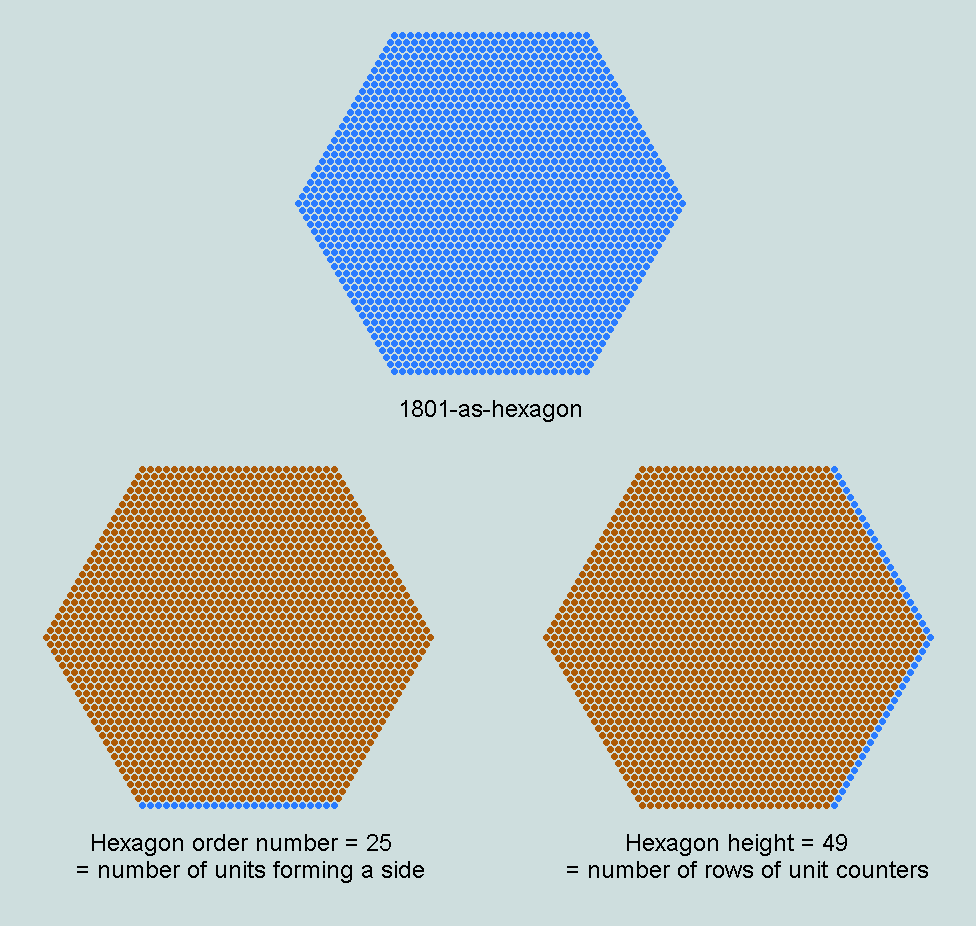
In the current context, the hexagon formed by the intersection of these triangles is of particular interest for its value (the number of counters involved in its representation) is the sum of the final 5 CVs of Genesis 1:1+ (i.e. 401 + 395 + 407 + 296 + 302 = 1801). It has already been observed that though 302 (the CV of the first word of Genesis 1:2) is not directly involved in the generating triangle 2701 (sum of the CVs of Genesis 1:1), the fact that both 1801-as-hexagon and 2701-as-triangle are perfectly inscribed by 703-as-triangle (sum of CVs 6 and 7) consolidates the link.

It transpires further that this particular numerical hexagon borders on the unique in that its order number (=25), height (49) and outline (=144) are all squares - and further, that the numbers of which they are squares are related thus, 5 + 7 = 12!

A computer simulation establishes the fact that, over Visual Basic's long-integer range there are just 4 more examples of numerical hexagons which are part-analogues of 1801. The following table provides the details: